Question

11．在Rt△ABC中，∠C=90°，∠A=30°，BD是∠ABC的平分线，若AC=b，则BD=（　　）

• A． $\frac{2b}{3}$
• B． $\frac{\sqrt{2}}{2}b$
• C． $\frac{\sqrt{3}}{2}b$
• D． $\frac{\sqrt{3}}{3}b$

Answer 1

分析 求BD的长应利用锐角三角函数算出和直角三角形有关的AD长和CD长即可．

解答 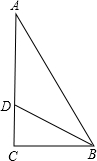解：在Rt△ABC中，∠C=90°，∠A=30°，所以∠ABC=60°，
∵BD是∠ABC的平分线，∴∠CBD=30°，
在Rt△ABC中，tan30°=$\frac{BC}{AC}$
∴$\frac{\sqrt{3}}{3}$=$\frac{BC}{b}$
∴BC=$\frac{\sqrt{3}}{3}$b
在Rt△CBD中，CD=BC•tan30°=$\frac{1}{3}$b，
∴AD=AC-CD=b-$\frac{1}{3}$b=$\frac{2}{3}$b，
∵∠A=∠ABD
∴BD=AD=$\frac{2}{3}$b．
故选A．

点评 本题考查了含30°的直角三角形的性质，解决本题的关键是得到所求的线段的相应线段的长度，主要应用了三角函数值．