
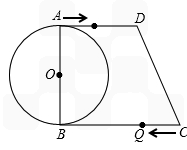
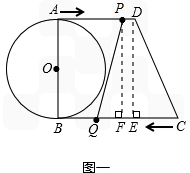
| 解:(1)过点D作DE⊥BC于E, ∵AB⊥BC, ∴四边形ADEB为矩形, ∴BE=AD=13,EC=3 又∵CD=5, ∴DE= 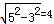 =4,即AB=4, =4,即AB=4,∴⊙O的半径为2cm; (2)当P、Q运动t秒时,AP=t,CQ=2t 则S四边形PQCD=y=  (13﹣t+2t)×4, (13﹣t+2t)×4,即y=2t+26(0≤t≤8) 当四边形PQCD为等腰梯形时,过P作PF⊥BC于F(如图一), 则有QF=CE=3 ∴2t﹣(13﹣t)=6, 则t= 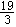 此时四边形PQCD面积y= 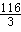 (cm2); (cm2);(3)存在.若PQ与圆相切,设切点为G,(如图二) 作PH⊥BC于H ∵A在⊙O上,∠A=90°, ∴AD切⊙O于A, ∵PQ切⊙O于G, ∴由切线长定理得:PG=PA=t.QG=QB=16﹣2t,QH=QB﹣BH=(16﹣2t)﹣t=16﹣3t PQ=QB+AP=16﹣t 在Rt△PQH中,PQ2=PH2+QH2, 即(16﹣t)2=16+(16﹣3t)2 ∴t2﹣8t+2=0, 解得 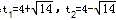 , ,∵0≤t≤8, ∴当 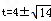 时,PQ与圆相切。 时,PQ与圆相切。 |
  |


科目:初中数学 来源: 题型:
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com