
分析 (1)①根据“纯利润=游客人数×票价-固定支出”可得;②利用①中所列解析式得出关于x的不等式,解不等式可得;
(2)先求出x≤1000时纯利润的最大值,可判断若要纯利达到19600时x>1000,再根据题意列出x>1000时的函数解析,根据解析式得出关于x的方程,解之可得.
解答 解:(1)①当x≤1000时,y=40(x-500)-725×4=40x-22900;
②根据题意得:40x-22900≥13000,
解得:x≥897.5,
∵每张团体票的售价x取整百数,
∴每张团体票的售价应不低于900元;
(2)当x≤1000时,y=40x-22900,
∵y随x的增大而增大,
∴当x=1000时,y最大=17100<19600,不符合题意,舍去;
当x>1000时,y=(x-500)(40-4×$\frac{x-1000}{100}$)-725×4
=-$\frac{1}{25}$x2+100x-42900
=-$\frac{1}{25}$(x-1250)2+19600,
当x=1250时,y最大=19600,
∴该旅行社每次发团的纯收入能达到19600元,
答:每张团体票的售价应定为1250元时,既能保证纯收入最高又能兼顾吸引顾客.
点评 本题主要考查二次函数的应用,理解题意判断出x的正确范围,并根据相等关系列出此范围内的函数解析式,利用二次函数的性质解题是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+$\frac{12}{5}$与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.
如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+$\frac{12}{5}$与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
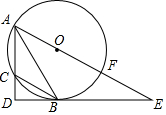 如图,已知△ABC是⊙O内接三角形,过点B作BD⊥AC于点D,连接AO并延长交⊙O于点F,交DB的延长线于点E,且点B是$\widehat{CF}$的中点.
如图,已知△ABC是⊙O内接三角形,过点B作BD⊥AC于点D,连接AO并延长交⊙O于点F,交DB的延长线于点E,且点B是$\widehat{CF}$的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-(-\frac{1}{5})$ | B. | $-|-\frac{1}{4}|$ | C. | ${(-\frac{1}{3})^2}$ | D. | $|-\frac{1}{6}|$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com