
【题目】如图①,在等边三角形ABC中.D是AB边上的动点,以CD为一边,向上作等边三角形EDC.连接AE.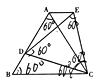
(1)求证:△DBC≌△EAC
(2)试说明AE∥BC的理由.
(3)如图②,当图①中动点D运动到边BA的延长线上时,所作仍为等边三角形,猜想是否仍有AE∥BC?若成立请证明.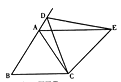
【答案】
(1)解:∵∠ACB=60 ![]() , ∠DCE=60
, ∠DCE=60 ![]() ,
,
∴∠BCD=60 ![]() -∠ACD, ∠ACE=60
-∠ACD, ∠ACE=60 ![]() -∠ACD,
-∠ACD,
即∠BCD=∠ACE,
在△DBC和△EAC中,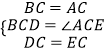 ,
,
∴△DBC≌△EAC(SAS)
(2)解:∵△DBC≌△EAC,
∴∠EAC=∠B=60 ![]() ,
,
又∵∠ACB=60 ![]() ,
,
∴∠EAC=∠ACB,
∴AE∥BC
(3)解:仍有AE∥BC,
∵△ABC,△EDC都为等边三角形,
∴BC=AC, DC=CE, ∠BCA=∠DCE=60 ![]() ,
,
∴∠BCA+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△DBC和△EAC中,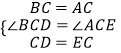 ,
,
∴△DBC和△EAC(SAS),
∴∠EAC=∠B=60 ![]() ,
,
又∵∠ACB=60 ![]() ,
,
∴∠EAC=∠ACB,
∴AE∥BC.
【解析】(1)根据已知条件△ABC和△EDC都是等边三角形,根据等边三角形的性质,得出边和角等于相等,再证明∠BCD=∠ACE,然后利用SAS证明△DBC≌△EAC即可。
(2)根据△DBC≌△EAC得出∠EAC=∠B=60 ° ,再利用等量代换证明∠EAC=∠ACB,然后根据平行线的判定即可证得结论。
(3)仍有AE∥BC,根据△ABC,△EDC都为等边三角形,得出BC=AC, DC=CE, ∠BCA=∠DCE,再证明∠BCD=∠ACE,就可证明△DBC和△EAC,然后再证明∠EAC=∠ACB,即可证得AE∥BC。


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
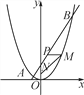
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念理解
如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)问题探究
①小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由。
②如图2,小红画了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将Rt△ABC沿
∠ABC的平分线BB'方向平移得到△A'B'C',连结AA',BC'.小红要是平移后的四边形ABC'A'是“等邻边四边形”,应平移多少距离(即线段BB'的长)?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com