
【题目】钓鱼岛是我国渤海海峡上的一颗明珠,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向钓鱼岛驶来,渔船向渔政部门报告,并立即返航.渔政船接到报告后,立即从该港口出发赶往钓鱼岛.下图是渔船及渔政船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)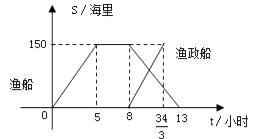
(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.
(2)求渔船和渔政船相遇时,两船与钓鱼岛的距离.
(3)在渔政船驶往钓鱼岛的过程中,求渔船从港口出发经过多长时间与渔政船相距30海里?
【答案】
(1)解:当0≤t≤5时,s=30;当5<t≤8时,s=150;当8<t≤13时,s=-30t+390
(2)解:渔政船离港口的距离与渔船离开港口的时间的函数关系式设为s=kt+b
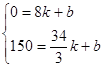 解得: k=45 b=-360 ∴s=45t-360
解得: k=45 b=-360 ∴s=45t-360
![]() 解得 t=10 s=90
解得 t=10 s=90
渔船离钓鱼岛距离为 150-90=60(海里)
(3)解:S渔=-30t+390 S渔政=45t-360
分两种情况:
遇之前,S渔-S渔政=30
-30t+390-(45t-360)=30
解得t= ![]() (或9.6)
(或9.6)
相遇之后,S渔政-S渔=30
45t-360-(-30t+390)=30
解得 t= ![]() (或10.4)
(或10.4)
∴当渔船离开港口9.6小时或10.4小时时,两船相距30海里.
【解析】(1)根据函数图像利用待定系数法求得函数的解析式;
(2)用待定系数法求得渔政船离港口的距离与渔船离开港口的时间的函数关系式,求两个函数解析式组成的方程组即可;
(3)根据渔船与渔政船相距30海里分两种情况:遇之前,S渔-S渔政=30 ,相遇之后,S渔政-S渔=30 ,即可列出方程求解。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校八年级(3)班体训队员的身高(单位:cm)如下:169,165,166,164,169,167,166,169,166,165,获得这组数据方法是( )
A.直接观察
B.查阅文献资料
C.互联网查询
D.测量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式从左到右的变形中,为因式分解的是( )
A.x(a﹣b)=ax﹣bx
B.x2﹣1+y2=(x﹣1)(x+1)+y2
C.y2﹣1=(y+1)(y﹣1)
D.ax+by+c=x(a+b)+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.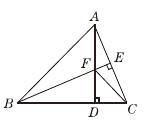
(1)求证:BF=2AE;
(2)若CD= ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com