
【题目】已知:如图,△ABC与△ADE,AB=AC,AD=AE,且∠BAC=∠DAE=40°,CD与BE相交于点F,连接AF则下列结论:①CD=BE:②△ABF≌△ACF;③∠BFD=140°;④FA平分∠BFD;⑤∠FAC=∠FAE.其中正确的结论有( )

A.2个B.3个C.4个D.5个
【答案】A
【解析】
根据已知条件易证△ABE≌△ACD,得到BE=CD即可判断①,根据两条边相等无法判断△ABF≌△ACF,根据已知条件不能得到∠BFC=40°,故可判断③,作AM⊥BE,AN⊥CD,根据全等三角形的性质得到AM=AN,可得AF平分∠BFD,故可判断④⑤.
∵∠BAC=∠DAE=40°,
∴∠BAC+∠CAE=∠DAE+∠CAE,
∴∠BAE=∠CAD,又AB=AC,AD=AE
∴△ABE≌△ACD
∴BE=CD,①正确;
∵AB=AC,AF=FA,∠BAF≠∠CAF,
∴△ABF与△ACF不全等,故②错误;
∴∠BAC≠∠BFC=40°,则∠BFD≠140°,③错误;
作AM⊥BE,AN⊥CD,∵△ABE≌△ACD
∴AM=AN,
∴AF平分∠BFD,AF不平分∠CAE,故④正确,⑤错误,
故选A.



科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,边AB、AC的垂直平分线分别交BC于E、F,若∠EAF=90°,AF=3,AE=4.
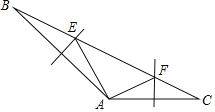
(1)求边BC的长;(2)求出∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某校七年级共有男生63名,为了参加全校运动会,七年级准备从本年级所有男生中挑选出身高相差不多的40名男生组成仪仗队,为此,收集到所有男生的身高数据(单位:cm),经过整理获得如下信息:
a.小明把所有男生的身高数据按由低到高整理为如下,但因为不小心有部分数据被墨迹遮挡:

b.小刚绘制了七年级所有男生身高的频数分布表
身高分组 | 划记 | 频数 |
149≤x<152 | 丅 | 2 |
152≤x<155 | 正一 | 6 |
155≤x<158 | 正正丅 | 12 |
158≤x<161 | 正正正 | 19 |
161≤x<164 | 正正 | 10 |
164≤x<167 | ______ | ______ |
167≤x<170 | ______ | ______ |
170≤x<173 | 丅 | 2 |
c.该校七年级男生身高的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 |
160 | m | n |
根据以上信息,回答下列问题:
(1)补全b表中频数分布表;
(2)直接写出c表中m,n的值;
(3)借助于已给信息,确定挑选出参加仪仗队的男生的身高范围;
(4)若本区七年级共有男生1260名,利用以上数据估计,全区七年级男生身高达到160及以上的男生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC的角平分线与BC的垂直平分线交与点D,DE⊥AB,DF⊥AC,垂足分别为E,F.若AB=10,AC=8.
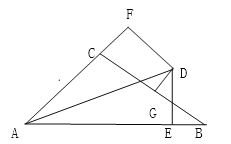
(1)求证:CF=BE;
(2) 求BE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中星星的颗数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
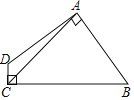
【题目】(1)己知:如图,△ABC,∠C=90°,现将斜边AB绕A点顺时针旋转90°到AD,过D点作DE⊥CA,交CA的延长线于点E.求证:△ABC ≌ △DAE
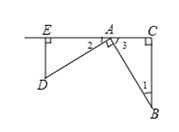
(2)如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写下表
序号 |
| 1 | 2 | … |
① |
| 5 |
| … |
② |
| 2 |
| … |
③ |
|
| 4 | … |
随着![]() 值的逐渐变大,回答下列问题
值的逐渐变大,回答下列问题
(1)当![]() 时,这三个代数式中 的值最小;
时,这三个代数式中 的值最小;
(2)你预计代数式的值最先超过1000的是代数式 ,此时![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24cm,CF=3cm,则制成整个金属框架所需这种材料的总长度为 ________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
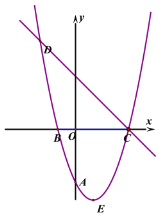
【题目】已知抛物线![]() 经过A(0,-3),B(-1,0),且抛物线对称轴为直线
经过A(0,-3),B(-1,0),且抛物线对称轴为直线![]() ,E
,E
是抛物线的顶点。
(1)求抛物线的解析式以及顶点坐标E。
(2)在![]() 轴上是否存在点P,使得
轴上是否存在点P,使得![]() 周长最短,若存在,请求出P点坐标,若不存在,请说
周长最短,若存在,请求出P点坐标,若不存在,请说
明理由。
(3)直线![]() 与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
使得![]() 的面积最大,若存在请求出最大面积,若不存在,请说明理由。
的面积最大,若存在请求出最大面积,若不存在,请说明理由。
(4)抛物线上是否存在点M,使得![]() 是直角三角形,若存在,直接写出M点坐标,若不
是直角三角形,若存在,直接写出M点坐标,若不
存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com