
【题目】(1)通过计算下列各式的值探究问题:
①![]() = ;
= ;![]() = ;
= ;![]() = ;
= ;![]() = .
= .
探究:对于任意非负有理数a,![]() = .
= .
②![]() = ;
= ;![]() = ;
= ;![]() = ;
= ;![]() = .
= .
探究:对于任意负有理数a,![]() = .
= .
综上,对于任意有理数a,![]() = .
= .
(2)应用(1)所得的结论解决问题:有理数a,b在数轴上对应的点的位置如图所示,化简:![]() -
-![]() -
-![]() +|a+b|.
+|a+b|.
![]()
科目:初中数学 来源: 题型:
【题目】一副含 ![]() 和
和 ![]() 角的三角板
角的三角板 ![]() 和
和 ![]() 叠合在一起,边
叠合在一起,边 ![]() 与
与 ![]() 重合,
重合, ![]() (如图1),点
(如图1),点 ![]() 为边
为边 ![]()
![]() 的中点,边
的中点,边 ![]() 与
与 ![]() 相交于点
相交于点 ![]() .现将三角板
.现将三角板 ![]() 绕点
绕点 ![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在 ![]() 从
从 ![]() 到
到 ![]() 的变化过程中,点
的变化过程中,点 ![]() 相应移动的路径长为 . (结果保留根号)
相应移动的路径长为 . (结果保留根号)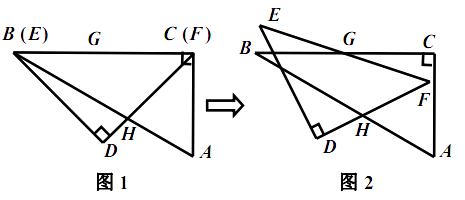
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1和∠2互为补角,∠A=∠D.求证:AB∥CD.
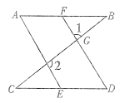
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(______).
又∠1和∠2互为补角(已知),
∴∠CGD和∠2互为补角,
∴AE∥FD(_________),
∴∠A=∠BFD(_______).
∵∠A=∠D(已知),
∴∠BFD=∠D(_______),
AB∥CD(______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次6元的包装费外,樱桃不超过1kg收费22元,超过1kg,则超出部分按每千克10元加收费用.设该公司从西安到南昌快递樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5kg樱桃,请你求出这次快寄的费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=12,弦AC=10,D是 ![]() 的中点,过点D作DE⊥AC,交AC的延长线于点E.
的中点,过点D作DE⊥AC,交AC的延长线于点E. 
(1)求证:DE是⊙O的切线;
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,根据设计要求,若∠EOF=45°,则此窗户的透光率(透光区域与矩形窗面的面积的比值)为 . 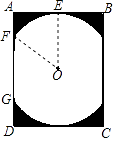
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
(1)在同一平面内,不相交的两条直线一定平行.(2)在同一平面内,不相交的两条线段一定平行.(3)相等的角是对顶角.(4)两条直线被第三条直线所截,同位角相等.(5)两条平行线被第三条直线所截,一对内错角的角平分线互相平行.其中,正确说法的个数是( )
A. 1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com