
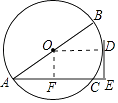
【题目】如图,已知⊙O的直径AB=12,弦AC=10,D是 ![]() 的中点,过点D作DE⊥AC,交AC的延长线于点E.
的中点,过点D作DE⊥AC,交AC的延长线于点E. 
(1)求证:DE是⊙O的切线;
(2)求AE的长.
【答案】
(1)证明:连接OD,
∵D为 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴∠BOD=∠BAE,
∴OD∥AE,
∵DE⊥AC,
∴∠ADE=90°,
∴∠AED=90°,
∴OD⊥DE,
则DE为圆O的切线;
(2)解:过点O作OF⊥AC,
∵AC=10,
∴AF=CF= ![]() AC=5,
AC=5,
∵∠OFE=∠DEF=∠ODE=90°,
∴四边形OFED为矩形,
∴FE=OD= ![]() AB,
AB,
∵AB=12,
∴FE=6,
则AE=AF+FE=5+6=11.
【解析】(1)连接OD,由D为弧BC的中点,得到两条弧相等,进而得到两个同位角相等,确定出OD与AE平行,利用两直线平行同旁内角互补得到OD与DE垂直,即可得证;(2)过O作OF垂直于AC,利用垂径定理得到F为AC中点,再由四边形OFED为矩形,求出FE的长,由AF+EF求出AE的长即可.
【考点精析】通过灵活运用勾股定理的概念和垂径定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】a、b是给定的整数,某同学分别计算x=-1,1,2,4时代数式ax+b的值,依次得到下列四个结果,已知其中3个是正确的,那么错误的是( )
A. ![]() B. a+b=5 C. 2a+b=7 D. 4a+b=14
B. a+b=5 C. 2a+b=7 D. 4a+b=14
查看答案和解析>>
科目:初中数学 来源: 题型:
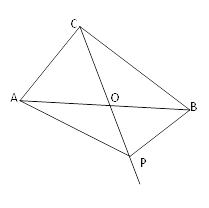
【题目】如图,在△ABC中,AB=2,AO=BO,P是直线CO上的一个动点,∠AOC=60°,当△PAB是以BP为直角边的直角三角形时,AP的长为( )
A. ![]() ,1,2 B.
,1,2 B. ![]() ,
,![]() ,2 C.
,2 C. ![]() ,
,![]() ,1 D.
,1 D. ![]() ,2
,2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点. 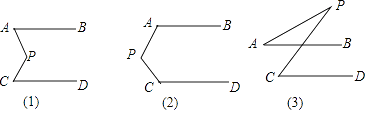
(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论;
(2)当点P移动到图(2)、图(3)的位置时,∠P、∠A、∠C又有怎样的关系?请分别写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B、C三地,A地在B、C两地之间.甲、乙两辆汽车分别从B、C两地同时出发,沿这条公路匀速相向行驶,甲匀速行驶1小时到达A地后继续以相同的速度向C处行驶,到达C后停止,乙匀速行驶1.2小时后到达A地并停止运动,甲、乙两车离A地的距离y1、y2(千米)与行驶时间x(时)的函数关系如图所示.
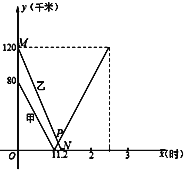
(1)BC的距离为 km
⑵求线段MN的函数表达式;
⑶求点P的坐标,并说明点P的实际意义;
⑷出发多长时间后,甲、乙相距60km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)通过计算下列各式的值探究问题:
①![]() = ;
= ;![]() = ;
= ;![]() = ;
= ;![]() = .
= .
探究:对于任意非负有理数a,![]() = .
= .
②![]() = ;
= ;![]() = ;
= ;![]() = ;
= ;![]() = .
= .
探究:对于任意负有理数a,![]() = .
= .
综上,对于任意有理数a,![]() = .
= .
(2)应用(1)所得的结论解决问题:有理数a,b在数轴上对应的点的位置如图所示,化简:![]() -
-![]() -
-![]() +|a+b|.
+|a+b|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣ ![]() ;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )
;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )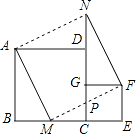
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B![]() ∠AEB
∠AEB![]() _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.
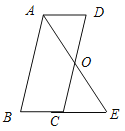
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,矩形OABC的边OA、OC分别落在x轴、y轴上,O为坐标原点,且OA=8,OC=4,连接AC,将矩形OABC对折,使点A与点C重合,折痕ED与BC交于点D,交OA于点E,连接AD,如图①. 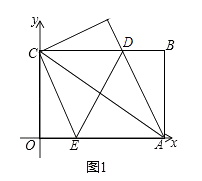
(1)求点D的坐标和AD所在直线的函数关系式;
(2)⊙M的圆心M始终在直线AC上(点A除外),且⊙M始终与x轴相切,如图②. 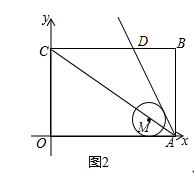
①求证:⊙M与直线AD相切;
②圆心M在直线AC上运动,在运动过程中,能否与y轴也相切?如果能相切,求出此时⊙M与x轴、y轴和直线AD都相切时的圆心M的坐标;如果不能相切,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com