
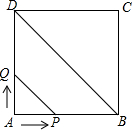
 如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C移动.设运动时间为x s,由点P、B、D、Q确定的图形的面积为y cm2,求y与x(0≤x≤8)之间的函数关系式.
如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C移动.设运动时间为x s,由点P、B、D、Q确定的图形的面积为y cm2,求y与x(0≤x≤8)之间的函数关系式. 分析 根据题意结合图形,分情况讨论:
①0≤x≤4时,根据四边形PBDQ的面积=△ABD的面积-△APQ的面积,列出函数关系式;
②4≤x≤8时,根据四边形PBDQ的面积=△BCD的面积-△CPQ的面积,列出函数关系式.
解答 解:①0≤x≤4时,
∵正方形的边长为4cm,
∴y=S△ABD-S△APQ,
=$\frac{1}{2}$×4×4-$\frac{1}{2}$•x•x,
=-$\frac{1}{2}$x2+8,
②4≤x≤8时,
y=S△BCD-S△CPQ,
=$\frac{1}{2}$×4×4-$\frac{1}{2}$•(8-x)•(8-x),
=-$\frac{1}{2}$(8-x)2+8.
综上所述,y=$\left\{\begin{array}{l}{-\frac{1}{2}{x}^{2}+8(0≤x≤4)}\\{-\frac{1}{2}(8-x)^{2}+8(4≤x≤8)}\end{array}\right.$.
点评 本题考查了动点问题函数关系,根据题意,分别求出两个时间段的函数关系式是解题的关键.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | x1=x2=2 | B. | x1=1,x2=6 | C. | x1=-3,x2=2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com