
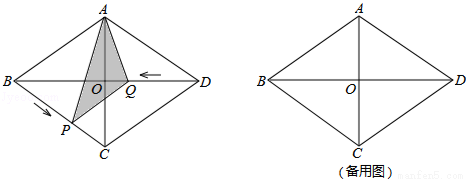
如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=6cm,BD=8cm,动点P,Q分别从点B,D同时出发,运动速度均为1cm/s,点P沿B→C→D运动,到点D停止,点Q沿D→O→B运动,到点O停止1s后继续运动,到B停止,连接AP,AQ,PQ.设△APQ的面积为y(cm2)(这里规定:线段是面积0的几何图形),点P的运动时间为x(s).
(1)填空:AB= cm,AB与CD之间的距离为 cm;
(2)当4≤x≤10时,求y与x之间的函数解析式;
(3)直接写出在整个运动过程中,使PQ与菱形ABCD一边平行的所有x的值.
(1)5, .
.
(2)当4≤x≤10时,y与x之间的函数解析式为:
y= .
.
(3)满足条件的x的值为 或
或 .
.
【解析】
试题分析:(1)根据勾股定理即可求得AB,根据面积公式求得AB与CD之间的距离.
(2)当4≤x≤10时,运动过程分为三个阶段,需要分类讨论,避免漏【解析】
①当4≤x≤5时,如答图1﹣1所示,此时点Q与点O重合,点P在线段BC上;
②当5<x≤9时,如答图1﹣2所示,此时点Q在线段OB上,点P在线段CD上;
③当9<x≤10时,如答图1﹣3所示,此时点Q与点B重合,点P在线段CD上.
(3)有两种情形,需要分类讨论,分别计算:
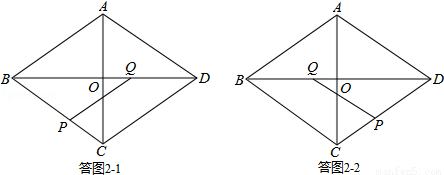
①若PQ∥CD,如答图2﹣1所示;
②若PQ∥BC,如答图2﹣2所示.
试题解析:(1)∵菱形ABCD中,AC=6cm,BD=8cm,
∴AC⊥BD,
∴AB= =5,
=5,
设AB与CD间的距离为h,
∴△ABC的面积S= AB•h,
AB•h,
又∵△ABC的面积S= S菱形ABCD=
S菱形ABCD= ×
× AC•BD=
AC•BD=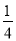 ×6×8=12,
×6×8=12,
∴ AB•h=12,
AB•h=12,
∴h= .
.
(2)设∠CBD=∠CDB=θ,则易得:sinθ=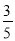 ,cosθ=
,cosθ= .
.
①当4≤x≤5时,如答图1﹣1所示,此时点Q与点O重合,点P在线段BC上.
∵PB=x,∴PC=BC﹣PB=5﹣x.
过点P作PH⊥AC于点H,则PH=PC•cosθ= (5﹣x).
(5﹣x).
∴y=S△APQ= QA•PH=
QA•PH= ×3×
×3× (5﹣x)=﹣
(5﹣x)=﹣ x+6;
x+6;
②当5<x≤9时,如答图1﹣2所示,此时点Q在线段OB上,点P在线段CD上.
PC=x﹣5,PD=CD﹣PC=5﹣(x﹣5)=10﹣x.
过点P作PH⊥BD于点H,则PH=PD•sinθ=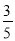 (10﹣x).
(10﹣x).
∴y=S△APQ=S菱形ABCD﹣S△ABQ﹣S四边形BCPQ﹣S△APD
=S菱形ABCD﹣S△ABQ﹣(S△BCD﹣S△PQD)﹣S△APD
= AC•BD﹣
AC•BD﹣ BQ•OA﹣(
BQ•OA﹣( BD•OC﹣
BD•OC﹣ QD•PH)﹣
QD•PH)﹣ PD×h
PD×h
= ×6×8﹣
×6×8﹣ (9﹣x)×3﹣[
(9﹣x)×3﹣[ ×8×3﹣
×8×3﹣ (x﹣1)•
(x﹣1)• (10﹣x)]﹣
(10﹣x)]﹣ (10﹣x)×
(10﹣x)×
=﹣ x2+
x2+ x﹣
x﹣ ;
;

③当9<x≤10时,如答图1﹣3所示,此时点Q与点B重合,点P在线段CD上.
y=S△APQ= AB×h=
AB×h= ×5×
×5×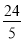 =12.
=12.
综上所述,当4≤x≤10时,y与x之间的函数解析式为:
y= .
.
(3)有两种情况:
①若PQ∥CD,如答图2﹣1所示.
此时BP=QD=x,则BQ=8﹣x.
∵PQ∥CD,
∴ ,即
,即 ,
,
∴x= ;
;
②若PQ∥BC,如答图2﹣2所示.
此时PD=10﹣x,QD=x﹣1.
∵PQ∥BC,
∴ ,即
,即 ,
,
∴x= .
.
综上所述,满足条件的x的值为 或
或 .
.
考点:1、菱形的性质;2、勾股定理;3、图形面积;4、相似


科目:初中数学 来源:2014年初中毕业升学考试(四川宜宾卷)数学(解析版) 题型:填空题
规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinx•cosy+cosx•siny.
据此判断下列等式成立的是 (写出所有正确的序号)
①cos(﹣60°)=﹣ ;
;
②sin75°=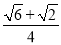 ;
;
③sin2x=2sinx•cosx;
④sin(x﹣y)=sinx•cosy﹣cosx•siny.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:解答题
如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:选择题
关于x的方程m(x+h)2+k=0(m,h,k均为常数,m≠0)的解是x1=﹣3,x2=2,则方程m(x+h﹣3)2+k=0的解是( )
A.x1=﹣6,x2=﹣1 B.x1=0,x2=5
C.x1=﹣3,x2=5 D.x1=﹣6,x2=2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:解答题
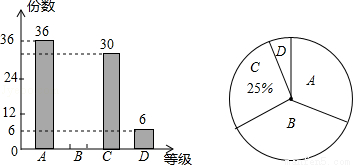
某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动,现从中随机抽取部分作品,按A,B,C,D四个等级进行评价,并根据结果绘制了如下两幅不完整的统计图.
(1)求抽取了多少份作品;
(2)此次抽取的作品中等级为B的作品有 ,并补全条形统计图;
(3)若该校共征集到800份作品,请估计等级为A的作品约有多少份.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:填空题
如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,连接PA,则∠PAB的度数可以是 (写出一个即可)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(北京卷)数学(解析版) 题型:解答题
根据某研究院公布的2009~2013年我国成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:
年份 | 年人均阅读图书数量(本) |
2009 |
|
2010 |
|
2011 |
|
2012 |
|
2013 |
|

根据以上信息解答下列问题:
(1)直接写出扇形统计图中 的值;
的值;
(2)从2009到2013年,成年国民年人均阅读图书的数量每年增长的幅度近似相等,估算2014年成年国民年人均阅读图书的数量约为 本;
(3)2013年某小区倾向图书阅读的成年国民有990人,若该小区2014年与2013年成年国民的人数基本持平,估算2014年该小区成年国民阅读图书的总数量约为 本.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(内蒙古呼和浩特卷)数学(解析版) 题型:选择题
下图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )

A.60π B.70π C.90π D.160π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com