
如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.

(1)抛物线的解析式为y=﹣ x2+
x2+ x+4;
x+4;
(2)线段PQ的最大值为 ;
;
(3)符合要求的点M的坐标为( ,9)和(
,9)和( ,﹣11).
,﹣11).
【解析】
试题分析:(1)如图1,易证BC=AC,从而得到点B的坐标,然后运用待定系数法求出二次函数的解析式;
(2)如图2,运用待定系数法求出直线AB的解析式.设点P的横坐标为t,从而可以用t的代数式表示出PQ的长,然后利用二次函数的最值性质就可解决问题;
(3)由于AB为直角边,分别以∠BAM=90°(如图3)和∠ABM=90°(如图4)进行讨论,通过三角形相似建立等量关系,就可以求出点M的坐标.
试题解析:(1)如图1,
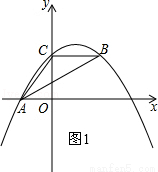
∵A(﹣3,0),C(0,4),
∴OA=3,OC=4.
∵∠AOC=90°,
∴AC=5.
∵BC∥AO,AB平分∠CAO,
∴∠CBA=∠BAO=∠CAB.
∴BC=AC.
∴BC=5.
∵BC∥AO,BC=5,OC=4,
∴点B的坐标为(5,4).
∵A(﹣3.0)、C(0,4)、B(5,4)在抛物线y=ax2+bx+c上,
∴
解得: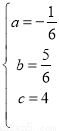
∴抛物线的解析式为y=﹣ x2+
x2+ x+4;
x+4;
(2)如图2,

设直线AB的解析式为y=mx+n,
∵A(﹣3.0)、B(5,4)在直线AB上,
∴
解得:
∴直线AB的解析式为y= x+
x+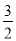 .
.
设点P的横坐标为t(﹣3≤t≤5),则点Q的横坐标也为t.
∴yP= t+
t+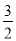 ,yQ=﹣
,yQ=﹣ t2+
t2+ t+4.
t+4.
∴PQ=yQ﹣yP=﹣ t2+
t2+ t+4﹣(
t+4﹣( t+
t+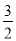 )
)
=﹣ t2+
t2+ t+4﹣
t+4﹣ t﹣
t﹣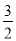
=﹣ t2+
t2+ +
+
=﹣ (t2﹣2t﹣15)
(t2﹣2t﹣15)
=﹣ [(t﹣1)2﹣16]
[(t﹣1)2﹣16]
=﹣ (t﹣1)2+
(t﹣1)2+ .
.
∵﹣ <0,﹣3≤1≤5,
<0,﹣3≤1≤5,
∴当t=1时,PQ取到最大值,最大值为 .
.
∴线段PQ的最大值为 ;
;
(3)①当∠BAM=90°时,如图3所示.

抛物线的对称轴为x=﹣ =﹣
=﹣ =
= .
.
∴xH=xG=xM= .
.
∴yG= ×
× +
+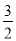 =
= .
.
∴GH= .
.
∵∠GHA=∠GAM=90°,
∴∠MAH=90°﹣∠GAH=∠AGM.
∵∠AHG=∠MHA=90°,∠MAH=∠AGM,
∴△AHG∽△MHA.
∴ .
.
∴ .
.
解得:MH=11.
∴点M的坐标为( ,﹣11).
,﹣11).
②当∠ABM=90°时,如图4所示.

∵∠BDG=90°,BD=5﹣ =
= ,DG=4﹣
,DG=4﹣ =
= ,
,
∴BG= .
.
同理:AG=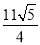 .
.
∵∠AGH=∠MGB,∠AHG=∠MBG=90°,
∴△AGH∽△MGB.
∴ .
.
∴ .
.
解得:MG= .
.
∴MH=MG+GH= +
+ =9.
=9.
∴点M的坐标为( ,9).
,9).
综上所述:符合要求的点M的坐标为( ,9)和(
,9)和( ,﹣11).
,﹣11).
考点:二次函数综合题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014年初中毕业升学考试(四川德阳卷)数学(解析版) 题型:解答题
如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y= (x>0)的图象经过矩形的对称中心E,且与边BC交于点 D.
(x>0)的图象经过矩形的对称中心E,且与边BC交于点 D.
(1)求反比例函数的解析式和点D的坐标;
(2)若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,求此直线的解析式.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川宜宾卷)数学(解析版) 题型:选择题
一个袋子中装有6个黑球3个白球,这些球除颜色外,形状、大小、质地等完全相同,在看不到球的条件下,随机地从这个袋子中摸出一个球,摸到白球的概率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川南充卷)数学(解析版) 题型:选择题
如图,将正方形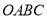 放在平面直角坐标系中,
放在平面直角坐标系中,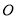 是原点,
是原点,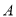 的坐标为(1,
的坐标为(1,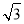 ),则点
),则点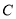 的坐标为( )
的坐标为( )
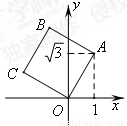
A.(-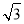 ,1) B.(-1,
,1) B.(-1,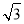 ) C.(
) C.(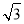 ,1) D.(-
,1) D.(-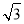 ,-1)
,-1)
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:填空题
如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C.若OC=2,则PC的长是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:解答题
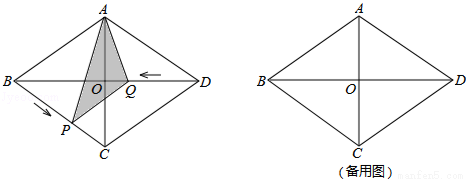
如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=6cm,BD=8cm,动点P,Q分别从点B,D同时出发,运动速度均为1cm/s,点P沿B→C→D运动,到点D停止,点Q沿D→O→B运动,到点O停止1s后继续运动,到B停止,连接AP,AQ,PQ.设△APQ的面积为y(cm2)(这里规定:线段是面积0的几何图形),点P的运动时间为x(s).
(1)填空:AB= cm,AB与CD之间的距离为 cm;
(2)当4≤x≤10时,求y与x之间的函数解析式;
(3)直接写出在整个运动过程中,使PQ与菱形ABCD一边平行的所有x的值.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(北京卷)数学(解析版) 题型:选择题
已知点 为某封闭图形边界上一定点,动点
为某封闭图形边界上一定点,动点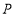 从点
从点 出发,沿其边界顺时针匀速运动一周.设点
出发,沿其边界顺时针匀速运动一周.设点 运动的时间为
运动的时间为 ,线段
,线段 的长为
的长为 .表示
.表示 与
与 的函数关系的图象大致如右图所示,则该封闭图形可能是
的函数关系的图象大致如右图所示,则该封闭图形可能是


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com