
如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y= (x>0)的图象经过矩形的对称中心E,且与边BC交于点 D.
(x>0)的图象经过矩形的对称中心E,且与边BC交于点 D.
(1)求反比例函数的解析式和点D的坐标;
(2)若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,求此直线的解析式.

(1)反比例函数解析式为y= ,点D的坐标为(1,2);
,点D的坐标为(1,2);
(2)直线的解析式为y=﹣2x+4或y=﹣ x+
x+ .
.
【解析】
试题分析:(1)根据中心对称求出点E的坐标,再代入反比例函数解析式求出k,然后根据点D的纵坐标与点B的纵坐标相等代入求解即可得到点D的坐标;
(2)设直线与x轴的交点为F,根据点D的坐标求出CD,再根据梯形的面积分两种情况求出OF的长,然后写出点F的坐标,再利用待定系数法求一次函数解析式求出直线解析式即可.
试题解析:(1)∵矩形OABC的顶点B的坐标是(4,2),E是矩形ABCD的对称中心,
∴点E的坐标为(2,1),
代入反比例函数解析式得,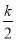 =1,
=1,
解得k=2,
∴反比例函数解析式为y= ,
,
∵点D在边BC上,
∴点D的纵坐标为2,
∴y=2时, =2,
=2,
解得x=1,
∴点D的坐标为(1,2);
(2)如图,

设直线与x轴的交点为F,
矩形OABC的面积=4×2=8,
∵矩形OABC的面积分成3:5的两部分,
∴梯形OFDC的面积为 ×8=3,
×8=3,
或 ×8=5,
×8=5,
∵点D的坐标为(1,2),
∴若 (1+OF)×2=3,
(1+OF)×2=3,
解得OF=2,
此时点F的坐标为(2,0),
若 (1+OF)×2=5,
(1+OF)×2=5,
解得OF=4,
此时点F的坐标为(4,0),与点A重合,
当D(1,2),F(2,0)时, ,
,
解得 ,
,
此时,直线解析式为y=﹣2x+4,
当D(1,2),F(4,0)时, ,
,
解得 ,
,
此时,直线解析式为y=﹣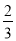 x+
x+ ,
,
综上所述,直线的解析式为y=﹣2x+4或y=﹣ x+
x+ .
.
考点:1.矩形的性质2.待定系数法求一次函数解析式3.待定系数法求反比例函数解析式.


科目:初中数学 来源:2014年初中毕业升学考试(四川眉山卷)数学(解析版) 题型:选择题
如图,直线 与x轴交于点B,双曲线
与x轴交于点B,双曲线 交于点A,过点B作x轴的垂线,与双曲线
交于点A,过点B作x轴的垂线,与双曲线 交于点C,且AB=AC,则k的值为( )
交于点C,且AB=AC,则k的值为( )
A.2 B.3 C.4 D.6

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川成都卷)数学(解析版) 题型:解答题
如图,在⊙O的内接△ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是 上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
(1)求证:△PAC∽△PDF;
(2)若AB=5, ,求PD的长;
,求PD的长;
(3)在点P运动过程中,设 ,求
,求 与
与 之间的函数关系式.(不要求写出
之间的函数关系式.(不要求写出 的取值范围)
的取值范围)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川德阳卷)数学(解析版) 题型:填空题
如图,△ABC中,∠A=60°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DE的度数为 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川德阳卷)数学(解析版) 题型:选择题
下列说法中正确的个数是( )
①不可能事件发生的概率为0;
②一个对象在实验中出现的次数越多,频率就越大;
③在相同条件下,只要试验的次数足够多,频率就可以作为概率的估计值;
④收集数据过程中的“记录结果”这一步,就是记录每个对象出现的频率.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川宜宾卷)数学(解析版) 题型:填空题
规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinx•cosy+cosx•siny.
据此判断下列等式成立的是 (写出所有正确的序号)
①cos(﹣60°)=﹣ ;
;
②sin75°=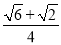 ;
;
③sin2x=2sinx•cosx;
④sin(x﹣y)=sinx•cosy﹣cosx•siny.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:解答题
如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com