Question

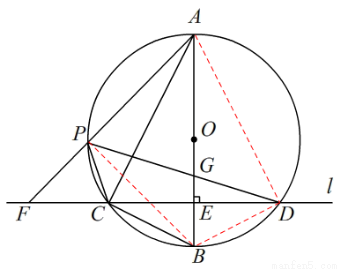
如图，在⊙O的内接△ABC中，∠ACB=90°，AC=2BC，过C作AB的垂线l交⊙O于另一点D，垂足为E.设P是 上异于A,C的一个动点，射线AP交l于点F，连接PC与PD，PD交AB于点G.

（1）求证：△PAC∽△PDF；

（2）若AB=5，，求PD的长；

（3）在点P运动过程中，设，求与之间的函数关系式.（不要求写出的取值范围）

 

 

Answer 1

（1）证明见解析；（2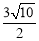）；（3）.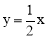

【解析】

试题分析：（1）应用圆周角定理证明∠APD＝∠FPC，得到∠APC＝∠FPD，又由∠PAC＝∠PDC，即可证明结论.

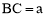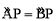（2）由AC=2BC，设，应用勾股定理即可求得BC，AC的长，则由AC=2BC得，由△ACE∽△ABC可求得AE，CE的长，由可知△APB是等腰直角三角形，从而可求得PA的长，由△AEF是等腰直角三角形求得EF=AE=4，从而求得DF的长，由（1）△PAC∽△PDF得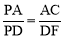，即可求得PD的长.

（3）连接BP，BD，AD，根据圆的对称性，可得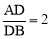，由角的转换可得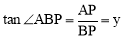，由△AGP∽△DGB可得 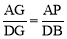，由△AGD∽△PGB可得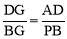，两式相乘可得结果.

试题解析：（1）由APCB内接于圆O，得∠FPC＝∠B，

又∵∠B＝∠ACE＝90°－∠BCE，∠ACE＝∠APD，∴∠APD＝∠FPC.

∴∠APD＋∠DPC＝∠FPC＋∠DPC，即∠APC＝∠FPD.

又∵∠PAC＝∠PDC，∴△PAC∽△PDF.

（2）连接BP，设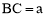，∵∠ACB=90°，AB=5，∴.∴.

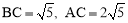∵△ACE∽△ABC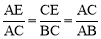，∴，即. ∴.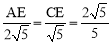

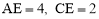∵AB⊥CD，∴.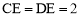

如图，连接BP，

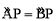∵，∴△APB是等腰直角三角形. ∴∠PAB＝45°，.

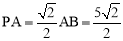∴△AEF是等腰直角三角形. ∴EF=AE=4. ∴DF=6.

由（1）△PAC∽△PDF得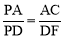，即.

∴PD的长为.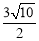

（3）如图，连接BP，BD，AD，

∵AC=2BC，∴根据圆的对称性，得AD=2DB，即.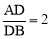

∵AB⊥CD，BP⊥AE，∴∠ABP＝∠AFD.

∵，∴.

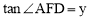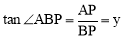∵△AGP∽△DGB，∴.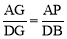

∵△AGD∽△PGB，∴.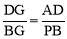

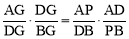∴，即.

∵，∴.

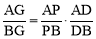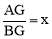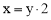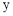∴与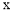之间的函数关系式为.

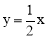考点：1.单动点问题；2.圆周角定理；3.相似三角形的判定和性质；4.勾股定理；5. 等腰直角三角形的判定和性质；6.垂径定理；7.锐角三角函数定义；8.由实际问题列函数关系式.