
��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣩����֪������y=x2+bx+c����A��4��0����B��1����3����
��1����b��c��ֵ����д���������ߵĶԳ���Ͷ������ꣻ
��2���������ߵĶԳ���Ϊֱ��l����P��m��n�������������ڵ�һ���ĵ㣬��E���P����ֱ��l�Գƣ���E���F����y��Գƣ����ı���OAPF�����Ϊ48�����P�����ꣻ
��3���ڣ�2���������£���M��ֱ��l������һ�㣬���ж�MP+MA�Ƿ������Сֵ�������ڣ���������Сֵ����Ӧ�ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
��1��b=��4��c=0�������ߵĶԳ���Ϊx=2������Ϊ��2����4����
��2����P��������6��12����
��3�����ڣ���СֵΪ6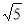 ��
��
��������
�����������1���ô���ϵ�����Ϳ����b��c���ٽ�����ʽ��ɶ���ʽ���Ϳ����ˣ�
��2��������֪�����ɵ�E��4��m��n����F��m��4��n�����Ӷ��õ�PF=4�������ı���OAPF�����Ϊ48�������P�������꣬Ȼ����������ߵĽ���ʽ�Ϳ������P�����꣮
��3�����ݵ�E���P����ֱ��l�Գƿɵ�MP=ME������MP+MA=ME+MA�����ɡ�����֮���߶���̡��ɵ�AE�ij�����MP+MA����Сֵ�����ù��ɶ����Ϳɽ�����⣮
�����������1����������y=x2+bx+c����A��4��0����B��1����3����
��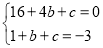 ��
��
��ã�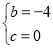 ��
��
��y=x2��4x=��x��2��2��4��
�������ߵĶԳ���Ϊx=2������Ϊ��2����4����
��2����ͼ1��
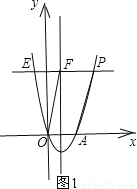
�ߵ�P��m��n�����E����ֱ��x=2�Գƣ�
���E��������4��m��n����
�ߵ�E���F����y��Գƣ�
���F��������m��4��n����
��PF=m����m��4��=4��
��PF=OA=4��
��PF��OA��
���ı���OAPF��ƽ���ı��Σ�
��S?OAPF=OA•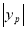 =4n=48��
=4n=48��
��n=12��
��m2��4m=n=12��
��ã�m1=6��m2=��2��
�ߵ�P�����������ڵ�һ���ĵ㣬
��m=6��
���P��������6��12����
��3������E��EH��x�ᣬ����ΪH����ͼ2��
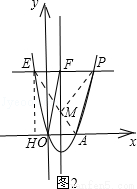
�ڣ�2���������£���P��6��12����E����2��12����
��AH=4������2��=6��EH=12��
��EH��x�ᣬ����EHA=90�㣬
��EA2=EH2+AH2=122+62=180��
��EA=6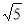 ��
��
�ߵ�E���P����ֱ��l�Գƣ�
��MP=ME��
��MP+MA=ME+MA��
���ݡ�����֮���߶���̡��ɵã�
����E��M��A����ʱ��MP+MA��С����Сֵ����EA�ij�����6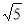 ��
��
���㣺1������ϵ������2���߶ε����ʣ�3�����ɶ�����4������x�ᡢy��ԳƵĵ�����꣮.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ����ݾ�����ѧ�������棩 ���ͣ������
ij��װ��Ԥ��һ��Ӧ�������ܳ����г�������8000Ԫ����һ�����������к��Ȼ����Ӧ��װ������17600Ԫ�����˵ڶ������ֳ��������������ǵ�һ������������2���������۹���8Ԫ���̼��������ֳ���ʱÿ�����۶���100Ԫ�����ʣ��10����8�����ۣ��ܿ����꣮�������������У��̼ҹ�ӯ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ�����������ѧ�������棩 ���ͣ�ѡ����
����������ȷ���ǣ�������
A��a3+a4=a7 B��2a3•a4=2a7 C����2a4��3=8a7 D��a8��a2=a4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ�üɽ������ѧ�������棩 ���ͣ�ѡ����
��ͼ��ֱ�� ��x�ύ�ڵ�B��˫����
��x�ύ�ڵ�B��˫���� ���ڵ�A������B��x��Ĵ��ߣ���˫����
���ڵ�A������B��x��Ĵ��ߣ���˫���� ���ڵ�C����AB=AC����k��ֵΪ�� ��
���ڵ�C����AB=AC����k��ֵΪ�� ��
A��2 B��3 C��4 D��6

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ�üɽ������ѧ�������棩 ���ͣ�ѡ����
һ���������£�3��6��7��2��3��4��3��6����ô�������ݵ���λ���������ֱ����� ��
A��3��3 B��3.5��3 C��4��3 D��3.5��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ����ξ�����ѧ�������棩 ���ͣ������
�������к�������y=2x��1����y= ����y=��x2��������ȡһ��������ȡ���ĺ���������������x��1ʱ������ֵy��x�������С���ĸ�����������
����y=��x2��������ȡһ��������ȡ���ĺ���������������x��1ʱ������ֵy��x�������С���ĸ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ����ξ�����ѧ�������棩 ���ͣ������
�Ȼ�������ֵ�� ��
��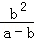 ������a=
������a=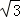 +1��b=
+1��b=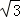 ��1��
��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ��ɶ�������ѧ�������棩 ���ͣ������
��ͼ������O���ڽ���ABC�У���ACB=90�㣬AC=2BC����C��AB�Ĵ���l����O����һ��D������ΪE.��P�� ������A,C��һ�����㣬����AP��l�ڵ�F������PC��PD��PD��AB�ڵ�G.
������A,C��һ�����㣬����AP��l�ڵ�F������PC��PD��PD��AB�ڵ�G.
��1����֤����PAC�ס�PDF��
��2����AB=5�� ����PD�ij���
����PD�ij���
��3���ڵ�P�˶������У��� ����
���� ��
�� ֮��ĺ�����ϵʽ.����Ҫ��д��
֮��ĺ�����ϵʽ.����Ҫ��д�� ��ȡֵ��Χ��
��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��Ĵ�����������ѧ�������棩 ���ͣ�ѡ����
����˵������ȷ�ĸ����ǣ�������
���������¼������ĸ���Ϊ0��
��һ��������ʵ���г��ֵĴ���Խ�࣬Ƶ�ʾ�Խ��
������ͬ�����£�ֻҪ����Ĵ����㹻�࣬Ƶ�ʾͿ�����Ϊ���ʵĹ���ֵ��
���ռ����ݹ����еġ���¼�������һ�������Ǽ�¼ÿ��������ֵ�Ƶ�ʣ�
A��1 B��2 C��3 D��4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com