孟建平错题本系列答案
超能学典应用题题卡系列答案科目：初中数学 来源： 题型：
设ω是一个平面图形，如果用直尺和圆规经过有限步作图（简称尺规作图），画出一个正方形与ω的面积相等（简称等积），那么这样的等积转化称为ω的“化方”．
⑴阅读填空
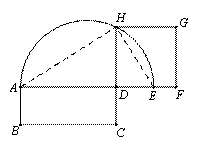
如图①，已知矩形ABCD，延长AD到E，使DE＝DC，以AE为直径作半圆．延长CD交半圆于点H，以DH为边作正方形DFGH，则正方形DFGH与矩形ABCD等积．
理由：连接AH，EH．
∵ AE为直径 ∴ ∠AHE＝90° ∴ ∠HAE＋∠HEA＝90°．
∵ DH⊥AE ∴ ∠ADH＝∠EDH＝90°
∴ ∠HAD＋∠AHD＝90°
∴ ∠AHD＝∠HED ∴ △ADH∽_____________．
∴ 
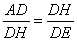，即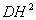
＝AD×DE．
又∵ DE＝DC ∴ 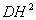＝____________，即正方形DFGH与矩形ABCD等积．
⑵操作实践
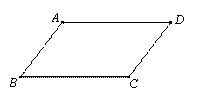
平行四边形的“化方”思路是，先把平行四边形转化为等积的矩形，再把矩形转化为等积的正方形．
如图②，请用尺规作图作出与□ABCD等积的矩形（不要求写具体作法，保留作图痕迹）．
⑶解决问题
三角形的“化方”思路是：先把三角形转化为等积的_________________（填写图形名称），再转化为等积的正方形．
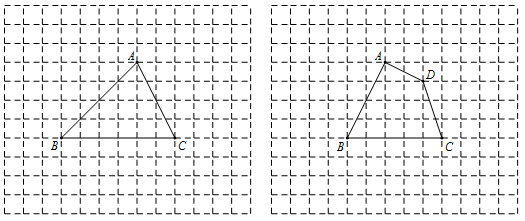
如图③，△ABC的顶点在正方形网格的格点上，请作出与△ABC等积的正方形的一条边（不要求写具体作法，保留作图痕迹，不通过计算△ABC面积作图）．
⑷拓展探究
n边形（n＞3）的“化方”思路之一是：把n边形转化为等积的n－1边形，…，直至转化为等积的三角形，从而可以化方．
如图④，四边形ABCD的顶点在正方形网格的格点上，请作出与四边形ABCD等积的三角形（不要求写具体作法，保留作图痕迹，不通过计算四边形ABCD面积作图）．
查看答案和解析>>
科目：初中数学 来源： 题型：
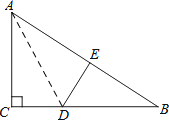
如
图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．
（1）求证：△BDE∽△BAC；
（2）已知AC=6，BC=8，求线段AD的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
下列说法错误的是（ ）
|
| A． | “伊利”纯牛奶消费者服务热线是4008169999，该十个数的中位数为7 |
|
| B． | 服装店老板最关心的是卖出服装的众数 |
|
| C． | 要了解全市初三近4万名学生2015年中考数学成绩情况，适宜采用全面调查 |
|
| D． | 条形统计图能够显示每组中的具体数据，易于比较数据之间的差别 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的倒数是（ ）
的图像是顶点坐标是 。
