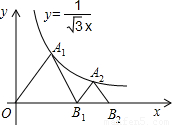
分析:分别过A
1、A
2作x轴的垂线,垂足分别为D、E,设OD=m,B
1E=n(m>0,n>0).根据等边三角形的性质和含30度的直角三角形三边的关系得到A
1D=
OD=
m,A
2E=
B
1E=
n,OE=2m+n,得到A
1的坐标为(m,
m),A
2的坐标为(2m+n,
n),然后先把A
1的坐标代入反比例解析式求得m的值,再把A
2的坐标代入反比例解析式得到n的值,这样就确定两等边三角形的边长,然后根据等边三角形的面积等于其边长的平方的
倍计算即可.
解答: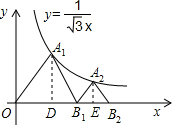
解:分别过A
1、A
2作x轴的垂线,垂足分别为D、E,如图,
设OD=m,B
1E=n(m>0,n>0).
∵△OA
1B
1,△B
1A
2B
2是等边三角形,
∴∠OA
1D=∠B
1A
2E=30°,
∴A
1D=
OD=
m,A
2E=
B
1E=
n,OE=2m+n,
∴A
1的坐标为(m,
m),A
2的坐标为(2m+n,
n),
又∵点A
1在函数y=
的图象上,
∴
m=
,解得m=
(m=-
舍去),
∴OB
1=2m=
,OE=
+n.
∵点A
2在函数y=
的图象上,
∴
n•(
+n)=
,解得n
1=
,n
2=
(舍去),
∴n=
,
∴B
1B
2=2n=
,
∴△OA
1B
1的面积=
OB
12=
×(
)
2=
,
△B
1A
2B
2的面积=
B
1B
22=
×[
]
2=
.
点评:本题考查了点在反比例函数图象上,则点的横纵坐标满足其解析式.也考查了含30度的直角三角形三边的关系以及等边三角形的性质.

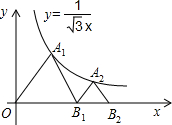 如图,△OA1B1,△B1A2B2是等边三角形,点A1,A2在函数y=
如图,△OA1B1,△B1A2B2是等边三角形,点A1,A2在函数y= 解:分别过A1、A2作x轴的垂线,垂足分别为D、E,如图,
解:分别过A1、A2作x轴的垂线,垂足分别为D、E,如图,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案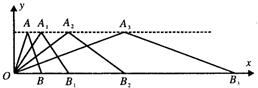 23、如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…
23、如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…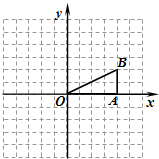 19、如图,网格小正方形的边长为1,△OAB为格点三角形(顶点都是格点),以O为坐标原点,OA所在直线为x轴建立平面直角坐标系.将△OAB绕点O按逆时针方向旋转90°得到△OA1B1.
19、如图,网格小正方形的边长为1,△OAB为格点三角形(顶点都是格点),以O为坐标原点,OA所在直线为x轴建立平面直角坐标系.将△OAB绕点O按逆时针方向旋转90°得到△OA1B1.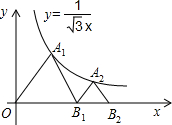 如图,△OA1B1,△B1A2B2是等边三角形,点A1,A2在函数y=
如图,△OA1B1,△B1A2B2是等边三角形,点A1,A2在函数y=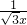 的图象上,点B1,B2在x轴的正半轴上,分别求△OA1B1,△B1A2B2的面积.
的图象上,点B1,B2在x轴的正半轴上,分别求△OA1B1,△B1A2B2的面积.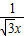 的图象上,点B1,B2在x轴的正半轴上,分别求△OA1B1,△B1A2B2的面积.
的图象上,点B1,B2在x轴的正半轴上,分别求△OA1B1,△B1A2B2的面积.