
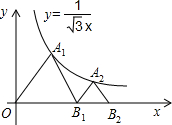 如图,△OA1B1,△B1A2B2是等边三角形,点A1,A2在函数y=
如图,△OA1B1,△B1A2B2是等边三角形,点A1,A2在函数y=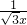 的图象上,点B1,B2在x轴的正半轴上,分别求△OA1B1,△B1A2B2的面积.
的图象上,点B1,B2在x轴的正半轴上,分别求△OA1B1,△B1A2B2的面积.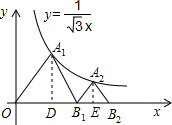 解:分别过A1、A2作x轴的垂线,垂足分别为D、E,如图,
解:分别过A1、A2作x轴的垂线,垂足分别为D、E,如图, OD=
OD= m,A2E=
m,A2E= B1E=
B1E= n,OE=2m+n,
n,OE=2m+n, m),A2的坐标为(2m+n,
m),A2的坐标为(2m+n, n),
n),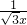 的图象上,
的图象上, m=
m= ,解得m=
,解得m= (m=-
(m=- 舍去),
舍去), ,OE=
,OE= +n.
+n.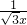 的图象上,
的图象上, n•(
n•( +n)=
+n)= ,解得n1=
,解得n1=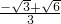 ,n2=
,n2=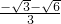 (舍去),
(舍去),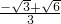 ,
,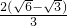 ,
, OB12=
OB12= ×(
×( )2=
)2= ,
, B1B22=
B1B22= ×[
×[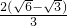 ]2=
]2=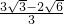 .
. OD=
OD= m,A2E=
m,A2E= B1E=
B1E= n,OE=2m+n,得到A1的坐标为(m,
n,OE=2m+n,得到A1的坐标为(m, m),A2的坐标为(2m+n,
m),A2的坐标为(2m+n, n),然后先把A1的坐标代入反比例解析式求得m的值,再把A2的坐标代入反比例解析式得到n的值,这样就确定两等边三角形的边长,然后根据等边三角形的面积等于其边长的平方的
n),然后先把A1的坐标代入反比例解析式求得m的值,再把A2的坐标代入反比例解析式得到n的值,这样就确定两等边三角形的边长,然后根据等边三角形的面积等于其边长的平方的 倍计算即可.
倍计算即可.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
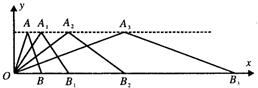 23、如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…
23、如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…查看答案和解析>>
科目:初中数学 来源: 题型:
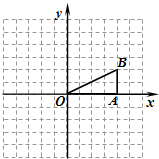 19、如图,网格小正方形的边长为1,△OAB为格点三角形(顶点都是格点),以O为坐标原点,OA所在直线为x轴建立平面直角坐标系.将△OAB绕点O按逆时针方向旋转90°得到△OA1B1.
19、如图,网格小正方形的边长为1,△OAB为格点三角形(顶点都是格点),以O为坐标原点,OA所在直线为x轴建立平面直角坐标系.将△OAB绕点O按逆时针方向旋转90°得到△OA1B1.查看答案和解析>>
科目:初中数学 来源: 题型:
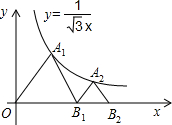 如图,△OA1B1,△B1A2B2是等边三角形,点A1,A2在函数y=
如图,△OA1B1,△B1A2B2是等边三角形,点A1,A2在函数y=| 1 | ||
|
查看答案和解析>>
科目:初中数学 来源:2008年浙江省宁波市余姚中学自主招生考试数学试卷(解析版) 题型:解答题
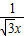 的图象上,点B1,B2在x轴的正半轴上,分别求△OA1B1,△B1A2B2的面积.
的图象上,点B1,B2在x轴的正半轴上,分别求△OA1B1,△B1A2B2的面积.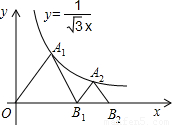
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com