
分析 (1)根据函数的对称轴x=2,此图象顶点的横坐标为2,此点在直线y=$\frac{1}{2}$x+1上,可求得y=(m2-2)x2-4mx+n的图象顶点坐标为(2,2).从而求得m=-1或m=2,利用最高点在直线上可得a<0,所以m=-1,n=-2,从而求得二次函数的表达式.
(2)首先假设顶点在直线y=x+1上移动到点M,设M(h,h+1),利用抛物线的开口方向不变,a=-1,得出二次函数的顶点式,再整理为一般形式,利用抛物线与x轴交点距离公式AB=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$求出h的值,进而得出二次函数的解析式即可.
解答 解:(1)∵二次函数的对称轴x=2,此图象顶点的横坐标为2,此点在直线y=$\frac{1}{2}$x+1上.
∴y=$\frac{1}{2}$×2+1=2.
∴y=(m2-2)x2-4mx+n的图象顶点坐标为(2,2).
∴-$\frac{-4m}{2({m}^{2}-2)}$=2.
解得m=-1或m=2.
∵最高点在直线上,∴a<0,
∴m=-1.
∴y=-x2+4x+n顶点为(2,2).
∴2=-4+8+n.∴n=-2.
则y=-x2+4x-2.
(2)因为顶点在直线y=x+1上移动到点M,设M(h,h+1),
因为抛物线的开口方向不变,a=-1,
设y=-(x-h)2+h+1,
=-x2+2hx-h2+h+1,
AB=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$=$\sqrt{△}$=$\sqrt{4h+4}$,
由S△ABM=8,
所以:$\frac{1}{2}$×$\sqrt{4h+4}$×(h+1)=8,
设$\sqrt{h+1}$=t,则$\sqrt{4h+4}$=2t,h+1=t2,
$\frac{1}{2}$×2t×t2=8,
则t3=8,
故t=2,即h=3,代入y=-x2+2hx-h2+h+1得,
故此时解析式为:y=-x2+6x+4.
点评 此题主要考查了二次函数的综合应用以及二次函数的性质,根据抛物线的平移不改变a的值以及抛物线与x轴交点距离公式AB=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$求出是解题关键..


科目:初中数学 来源: 题型:填空题
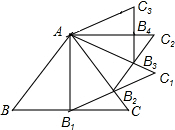 如图,等边△ABC的边长为2,以BC边上的高AB1为边作等边△AB1C1,B1C1交AC于点B2,△AB1B2的面积记做S1;再以AB2为边作等边△AB2C2,B2C2交AC1于点B3,△AB2B3的面积记做S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$..
如图,等边△ABC的边长为2,以BC边上的高AB1为边作等边△AB1C1,B1C1交AC于点B2,△AB1B2的面积记做S1;再以AB2为边作等边△AB2C2,B2C2交AC1于点B3,△AB2B3的面积记做S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$..查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 单程所花时间 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| 人数 | 6 | 6 | 8 | 14 | 5 | 4 | 1 | 1 |
| A. | 15 | B. | 20 | C. | 25 | D. | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≥0 | B. | m≤0 | C. | m≠1 | D. | m≤0且m≠-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
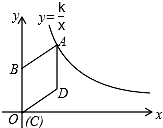 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥$\frac{3}{4}$ | B. | x≤$\frac{3}{4}$ | C. | x<$\frac{3}{4}$ | D. | x≠$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
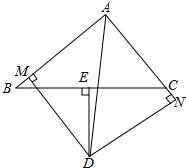 如图,△ABC中,E是BC边上的中点,DE⊥BC于E,交∠BAC的平分线AD于D,过D点作DM⊥AB于M,作DN⊥AC于N,试证明:BM=CN.
如图,△ABC中,E是BC边上的中点,DE⊥BC于E,交∠BAC的平分线AD于D,过D点作DM⊥AB于M,作DN⊥AC于N,试证明:BM=CN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com