AE∥BF且AE=BF 12cm
2 60
分析:(1)根据AB=AC,△FEC是由△ABC绕点C顺时针旋转180°产生的,可知,AC=CF,BC=CE,所以得到四边形ABFE是平行四边形;由平行四边形的性质可知AE∥BF且AE=BF;
(2)由于BC=CE,所以△ABC与△ACE可看作等底同高的两个三角形,那么S
△ABC=S
△ACE;由于AC=CF,同理,S
△ABC=S
△FBC,S
△ACE=S
△FCE;即四个三角形的面积相等,所以S
四边形ABFE=4×S
△ABC,可求得面积是12cm
2;
(3)当∠ACB=60°时,AB=AC=BC,可得AF=BE,即四边形ABFE是矩形.
解答:(1)∵△FEC是△ABC顺时针旋转180°产生的,且AB=AC,
∴ACF、BCE共线且AC=CF,BC=CE,
∴四边形ABFE是平行四边形,
∴AB∥BF且AB=BF.
(2)∵BC=CE,
∴△ABC与△ACE可看作等底同高的两个三角形,
∴S
△ABC=S
△ACE;
又∵AC=CF,
同理,S
△ABC=S
△FBC,S
△ACE=S
△FCE;
∴S
四边形ABFE=4×S
△ABC=12cm
2.
(3)当∠ACB=60°时,四边形ABFE是矩形.理由如下:
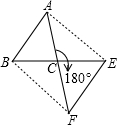
∵∠ACB=60°时,AB=AC,
∴AB=AC=BC,
又∵AC=CF,BC=CE,
∴AF=BE,
∴平行四边形ABFE是矩形.
点评:本题主要考查了矩形的判定,等腰三角形的性质和中心对称图形的性质.解题的关键是利用中心对称图形的性质得到相等的线段和全等的图形.熟练掌握矩形的判定以及等腰三角形的性质才能在综合题中灵活运用.

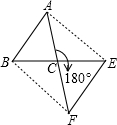 如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.则AE与BF的关系是________;若△ABC的面积为3cm2,则四边形ABFE的面积是________;当∠ACB为________度时,四边形ABFE为矩形.
如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.则AE与BF的关系是________;若△ABC的面积为3cm2,则四边形ABFE的面积是________;当∠ACB为________度时,四边形ABFE为矩形.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为