
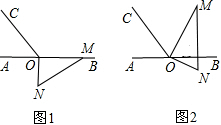
 如图1,点O为直线AB上一点,过O点作直线OC,使∠BOC=120°,将一块 含30°,60°的直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在直线AB下方.
如图1,点O为直线AB上一点,过O点作直线OC,使∠BOC=120°,将一块 含30°,60°的直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在直线AB下方.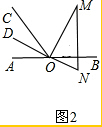
| 225 |
| 6 |

| 90 |
| 6 |
| 270 |
| 6 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
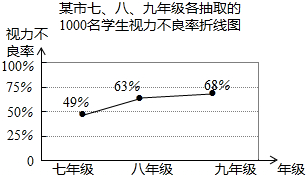
查看答案和解析>>
科目:初中数学 来源: 题型:
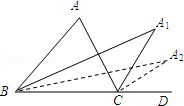 如图,在△ABC中,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…∠A2013BC与∠A2013CD的平分线相交于点A2014,得∠A2014,根据题意填空:
如图,在△ABC中,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…∠A2013BC与∠A2013CD的平分线相交于点A2014,得∠A2014,根据题意填空:查看答案和解析>>
科目:初中数学 来源: 题型:
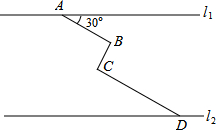 如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:
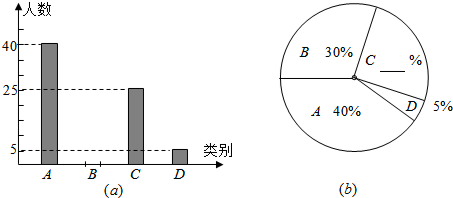
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
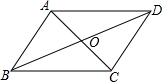 如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形
如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com