
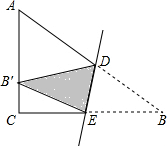
 在Rt△ABC中,∠C=90°,AC=6,BC=8,将△BDC沿直线DE折叠,使B落在AC的三等分点B′处,求CE的长.
在Rt△ABC中,∠C=90°,AC=6,BC=8,将△BDC沿直线DE折叠,使B落在AC的三等分点B′处,求CE的长.| 15 |
| 2 |
| 15 |
| 2 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
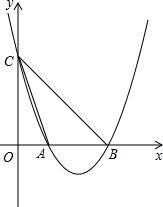 如图,已知抛物线y=ax2+bx+c经过A(2,0),B(6,0),C(0,6),其对称轴交x轴于M点,
如图,已知抛物线y=ax2+bx+c经过A(2,0),B(6,0),C(0,6),其对称轴交x轴于M点,查看答案和解析>>
科目:初中数学 来源: 题型:
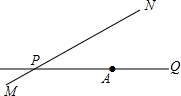 如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行驶时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶.学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行驶时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶.学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?查看答案和解析>>
科目:初中数学 来源: 题型:
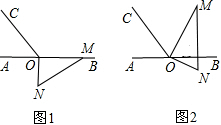 如图1,点O为直线AB上一点,过O点作直线OC,使∠BOC=120°,将一块 含30°,60°的直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在直线AB下方.
如图1,点O为直线AB上一点,过O点作直线OC,使∠BOC=120°,将一块 含30°,60°的直角三角板的直角顶点放在O处,一边OM在射线OB上,另一边ON在直线AB下方.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com