
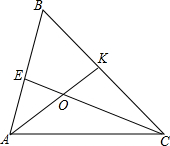
 如图,在△ABC中,∠B=60°,角平分线AK,CE的交点为O.求证:OK=OE.
如图,在△ABC中,∠B=60°,角平分线AK,CE的交点为O.求证:OK=OE.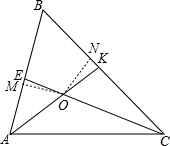 证明:如图,过O作OM⊥AB,ON⊥BC,垂足分别为M、N,
证明:如图,过O作OM⊥AB,ON⊥BC,垂足分别为M、N,
|


科目:初中数学 来源: 题型:
| A、8(1+x)2=10 |
| B、8(1-x)2=10 |
| C、8+8×2x=10 |
| D、8+8x2=10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
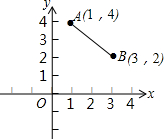 “西气东输”惠及千家万户,使许多的农村家庭也告别了以植物秸秆为主要原料的时代,使用上了天然气,如图所示,天然气的主要管道在x轴所在的位置,现拟在该主要管道上新建一气站为图中的A,B两村庄的农户供气,请你帮助确定该供气站建在何处时,到两村所铺设的管道最短,最少需要管道多少千米?
“西气东输”惠及千家万户,使许多的农村家庭也告别了以植物秸秆为主要原料的时代,使用上了天然气,如图所示,天然气的主要管道在x轴所在的位置,现拟在该主要管道上新建一气站为图中的A,B两村庄的农户供气,请你帮助确定该供气站建在何处时,到两村所铺设的管道最短,最少需要管道多少千米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com