
科目:初中数学 来源: 题型:解答题
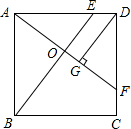 如图所示,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.
如图所示,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
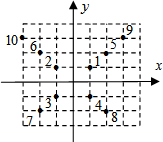 如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )
如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,抛物线y=ax2+bx+c与坐标轴的交点为A、B、C,且OA=OC=1,则下列关系中正确的是( )
如图,抛物线y=ax2+bx+c与坐标轴的交点为A、B、C,且OA=OC=1,则下列关系中正确的是( )| A. | a+b=-1 | B. | ac<0 | C. | b<2a | D. | a-b=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
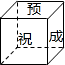 李明为好友制作一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,期中“预”的对面是“中”,“正”的对面是“功”,则它的平面展开图可能是( )
李明为好友制作一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,期中“预”的对面是“中”,“正”的对面是“功”,则它的平面展开图可能是( )| A. | 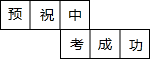 | B. | 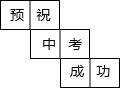 | C. | 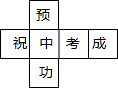 | D. | 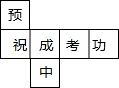 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com