
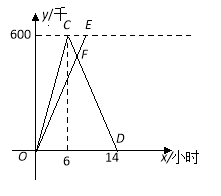
°æƒø°øA£¨B¡Ω≥«œýæý600«ß√◊£¨º◊°¢““¡Ω≥µÕ¨ ±¥”A≥«≥ˆ∑¢ ªœÚB≥«£¨º◊≥µµΩ¥ÔB≥«∫Û¡¢º¥∑µªÿ£Æ»ÁÕº «À¸√«¿ÎA≥«µƒæý¿Îy£®«ß√◊£©”Ζ– ª ±º‰ x£®–° ±£©÷ƺ‰µƒ∫Ø ˝ÕºœÛ£Æ
£®1£©«Ûº◊≥µ–– ªπ˝≥Ã÷–y”Îx÷ƺ‰µƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢–¥≥ˆ◊‘±‰¡øxµƒ»°÷µ∑∂Œß£ª
£®2£©µ±À¸√«–– ª¡À7–° ± ±£¨¡Ω≥µœý”ˆ£¨«Û““≥µµƒÀŸ∂»º∞““≥µ–– ªπ˝≥Ã÷–y”Îx÷ƺ‰µƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢–¥≥ˆ◊‘±‰¡øxµƒ»°÷µ∑∂Œß£ª
£®3£©µ±¡Ω≥µœýæý100«ß√◊ ±£¨«Ûº◊≥µ–– ªµƒ ±º‰.
°æ¥∞∏°ø£®1£©œÍº˚Ω‚Œˆ£®2£©œÍº˚Ω‚Œˆ£®3£©œÍº˚Ω‚Œˆ
°æΩ‚Œˆ°ø
‘Â∑÷Œˆ£∫£®1£©œ»∏˘æðÕºœÛ∫Õ“‚÷™µ¿£¨º◊ «∑÷∂Œ∫Ø ˝£¨À˘“‘∑÷±…Ë0°Ðx°Ð6 ±£¨y=k1x£ª6£ºx°Ð14 ±£¨y=kx+b£¨∏˘æðÕºœÛ…œµƒµ„µƒ◊¯±Í£¨¿˚”√¥˝∂®œµ ˝∑®ø…«ÛΩ‚£Æ
£®2£©◊¢“‚œý”ˆ ± «‘⁄6-14–° ±÷ƺ‰£¨«ÛΩªµ„ ±”¶∏√Ã◊”√º◊÷–µƒ∫Ø ˝πÿœµ ΩŒ™y=-75x+1050£¨÷±Ω”∞—x=7¥˙»Îº¥ø…«Ûœý”ˆ ±yµƒ÷µ£¨‘Ÿ«ÛÀŸ∂»º¥ø…£Æ
£®3£©∏˘æð“‚£¨”…ÕºœÒø…µ√∑÷∂Œµƒ∑∂Œß£¨»ª∫Û¡–≤ªµ» Ω£¨∑÷±«ÛΩ‚º¥ø….
‘Ã‚Ω‚Œˆ£∫£®1£©![]() =
=![]() .
.
£®2£©x=7 ±£¨y=525, °ý![]() («ß√◊/–° ±)£ª
(«ß√◊/–° ±)£ª![]() =75x(0°Ðx°Ð8).
=75x(0°Ðx°Ð8).
(3)…Ë¡Ω≥µ÷ƺ‰µƒæý¿ÎŒ™W£®«ß√◊£©£¨‘ÚW”Îx÷ƺ‰µƒ∫Ø ˝πÿœµ ΩŒ™£∫
W= £¨µ±W=100 ±£¨«Ûµ√x=4ªÚ
£¨µ±W=100 ±£¨«Ûµ√x=4ªÚ![]() ªÚ
ªÚ![]() .π º◊≥µ–– ªµƒ ±º‰Œ™4–° ±ªÚ
.π º◊≥µ–– ªµƒ ±º‰Œ™4–° ±ªÚ![]() –° ±ªÚ
–° ±ªÚ![]() –° ±.
–° ±.


 √˚ÂΩæÌœµ¡–¥∞∏
√˚ÂΩæÌœµ¡–¥∞∏ ”≈º”æ´æÌœµ¡–¥∞∏
”≈º”æ´æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂˛¥Œ∫Ø ˝y=x2+2x©Å1µƒ◊Ó–°÷µ «£® £©
A.©Å1
B.©Å2
C.1
D.2
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨°œC=90°„£¨ABµƒ¥π÷±∆Ω∑÷œþDEΩªAC”⁄D£¨¥π◊„Œ™E£¨»Ù°œA=30°„£¨CD=3£Æ
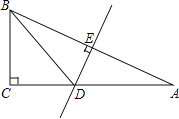
£®1£©«Û°œBDCµƒ∂» ˝£Æ
£®2£©«ÛACµƒ≥§∂»£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ´≈◊ŒÔœþy=x2œÚ◊Û∆Ω“∆2∏ˆµ•Œª≥§∂»£¨‘ŸœÚœ¬∆Ω“∆3∏ˆµ•Œª≥§∂»£¨µ√µΩµƒ≈◊ŒÔœþµƒ∫Ø ˝±Ì¥Ô ΩŒ™£® £©
A.y=£®x+2£©2©Å3
B.y=£®x+2£©2+3
C.y=£®x©Å2£©2+3
D.y=£®x©Å2£©2©Å3
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø-64µƒ¡¢∑Ω∏˘ «_____£Æµ„A(0£¨3)œÚ”“∆Ω“∆2∏ˆµ•Œª≥§∂»∫ÛÀ˘µ√µƒµ„A°‰µƒ◊¯±ÍŒ™_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Ù|a©Å4|=|a|+|©Å4|£¨‘Úaµƒ÷µ «£®°°°°£©
A. »Œ“‚”–¿Ì ˝ B. »Œ“‚“ª∏ˆ∑«∏∫ ˝
C. »Œ“‚“ª∏ˆ∑«’˝ ˝ D. »Œ“‚“ª∏ˆ∏∫ ˝
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ´≈◊ŒÔœþy=2x2œÚ◊Û∆Ω“∆1∏ˆµ•Œª£¨‘ŸœÚœ¬∆Ω“∆2∏ˆµ•Œª£¨µ√µΩµƒ≈◊ŒÔœþ «£® £©
A.y=2£®x+1£©2+2
B.y=2£®x©Å1£©2+2
C.y=2£®x©Å1£©2©Å2
D.y=2£®x+1£©2©Å2
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®6 ∑÷£©Œ™¡Àº”«øπ´√ÒµƒΩ⁄ÀÆ“‚ ∂£¨∫œ¿Ì¿˚”√ÀÆ◊ ‘¥£¨ƒ≥ –≤…”√º€∏Òµ˜øÿµƒ ÷∂Œ¥ÔµΩΩ⁄ÀƵƒƒøµƒ£¨∏√ –◊‘¿¥ÀÆ ’∑—µƒ ’∑—±Í◊º»Áœ¬±Ì£∫
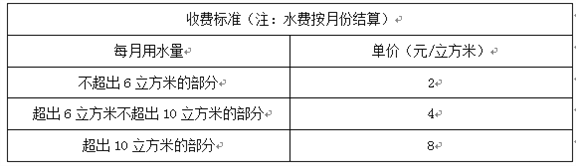
¿˝»Á£∫ƒ≥ªßæ”√Ò1‘¬∑ð”√ÀÆ8¡¢∑Ω√◊£¨”¶ ’ÀÆ∑—Œ™2°¡6+4°¡(8-6)=20£®‘™£©£Æ
«Î∏˘æð…œ±Ìµƒƒ⁄»ðΩ‚¥œ¬¡–Œ £∫
¢≈»Ùƒ≥ªßæ”√Ò2‘¬∑ð”√ÀÆ5¡¢∑Ω√◊£¨‘Ú”¶ ’ÀÆ∑—________‘™£ª
¢∆»Ùƒ≥ªßæ”√Ò3‘¬∑ðΩªÀÆ∑—36‘™£¨‘Ú”√ÀÆ¡øŒ™________¡¢∑Ω√◊£ª
¢«»Ùƒ≥ªßæ”√Ò4‘¬∑ð”√ÀÆa¡¢∑Ω√◊£®∆‰÷–6<a<10£©£¨«Î”√∫¨aµƒ¥˙ ˝ Ω±Ì æ”¶ ’ÀÆ∑—________‘™£Æ
¢»»Ùƒ≥ªßæ”√Ò 5°¢6 ¡Ω∏ˆ‘¬π≤”√ÀÆ18¡¢∑Ω√◊£®6‘¬∑ð”√ÀÆ¡ø≥¨π˝¡À10¡¢∑Ω√◊£©£¨…Ë5‘¬∑ð”√ÀÆx¡¢∑Ω√◊£¨«Î”√∫¨xµƒ¥˙ ˝ Ω±Ì æ∏√æ”√Ò5°¢6¡Ω∏ˆ‘¬π≤ΩªÀÆ∑—∂ý…Ÿ‘™£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com