
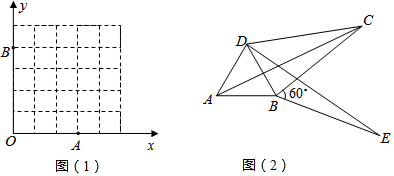
分析 (1)由于∠AOB=90°,则OB2+OA2=AB2=25,则找出格点M使它到O点的距离为5(坐标轴上除外)可得到满足条件的四边形OAMB;
(2)连接CE,如图(2),利用旋转的性质得DE=AC,BC=BE,∠CBE=60°,则可判断△BCE为等边三角形,所以BC=CE,∠BCE=60°,再证明∠DCE=90°,然后利用勾股定理得到DC2+EC2=DE2,从而得到
DC2+BC2=AC2.
解答 解:(1)如图(1),四边形OAMB或四边形OAM′B为所作;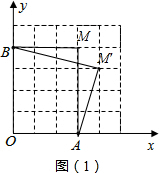
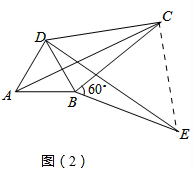
(2)连接CE,如图(2),
∵△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,
∴DE=AC,BC=BE,∠CBE=60°,
∴△BCE为等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2,
即四边形ABCD是勾股四边形.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了阅读理解能力.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -4 | B. | 4 | C. | 4或-4 | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
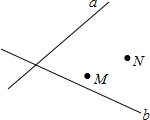 a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置(不写作法,保留作图痕迹).
a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置(不写作法,保留作图痕迹).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com