
【题目】某绿色种植基地种植的农产品喜获丰收,此基地将该农产品以每千克5元出售,这样每天可售出1500千克,但由于同类农产品的大量上市,该基地准备降价促销,经调查发现,在本地该农产品若每降价![]() 元,每天可多售出100千克
元,每天可多售出100千克![]() 当本地销售单价为
当本地销售单价为![]() 元时,销售量为y千克.
元时,销售量为y千克.
![]() 请直接写出y和x的函数关系式;
请直接写出y和x的函数关系式;
![]() 求在本地当销售单价为多少时可以获得最大销售收入?最大销售收入是多少?
求在本地当销售单价为多少时可以获得最大销售收入?最大销售收入是多少?
![]() 若该农产品不能在一周内出售,将会因变质而不能出售
若该农产品不能在一周内出售,将会因变质而不能出售![]() 依此情况,基地将10000千克该农产品运往外地销售
依此情况,基地将10000千克该农产品运往外地销售![]() 已知这10000千克农产品运到了外地,并在当天全部售完
已知这10000千克农产品运到了外地,并在当天全部售完![]() 外地销售这种农产品的价格比在本地取得最大销售收入时的单价还高
外地销售这种农产品的价格比在本地取得最大销售收入时的单价还高![]() ,而在运输过程中有
,而在运输过程中有![]() 损耗,这样这一天的销售收入为42000元
损耗,这样这一天的销售收入为42000元![]() 请计算出a的值.
请计算出a的值.
科目:初中数学 来源: 题型:
【题目】阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为a,b,c,记![]() ,那么三角形的面积为
,那么三角形的面积为![]() . ①
. ①
古希腊几何学家海伦(Heron,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约1202﹣﹣约1261),曾提出利用三角形的三边求面积的秦九韶公式: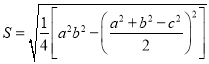 . ②
. ②
下面我们对公式②进行变形: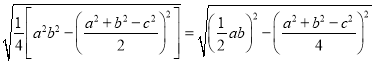

![]()
![]()
![]()
![]() .
.
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦﹣﹣秦九韶公式.
问题:如图,在△ABC中,AB=13,BC=12,AC=7,⊙O内切于△ABC,切点分别是D、E、F.

(1)求△ABC的面积;
(2)求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要________个小立方块.最终搭成的长方体的表面积是________.
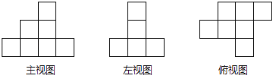
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P的对面是一面东西走向的墙,某人在点P观察一辆自西向东行驶的汽车AB,汽车的长为6米,根据图中标示的数据解决下列问题:
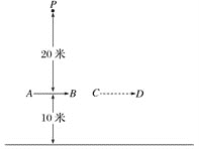
(1)画出此人在汽车与墙之间形成的盲区,并求出该盲区的面积;
(2)当汽车行驶到CD位置时,盲区的面积是否会发生变化?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
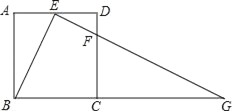
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF:DC=1:4,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为10,求BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com