
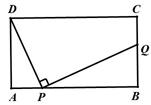
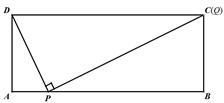
 ,
,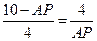 ,∴
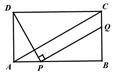
,∴ 或8,∴存在点P使得点Q与点C重合,出此时AP的长2 或8.
或8,∴存在点P使得点Q与点C重合,出此时AP的长2 或8.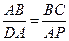 ,即
,即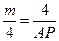 ,∴
,∴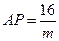 .
.
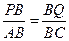 ,即
,即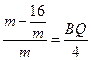 ,∴
,∴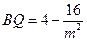 .
.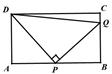
 ,
,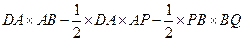
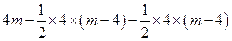 =16(4<
=16(4<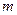 ≤8).
≤8).

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

 (B)5
(B)5 (C)5 (D)10
(C)5 (D)10查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.对角线相等的四边形是矩形 | B.对角线互相平分的四边形是矩形 |
| C.矩形的对角线互相垂直且平分 | D.矩形的对角线相等且互相平分 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 珠海)(本题满分6分)如图,在正方形ABC1D1中,AB=1.连接AC1,
珠海)(本题满分6分)如图,在正方形ABC1D1中,AB=1.连接AC1,
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 的值等于多少时.△PFD∽△BFP?并说明理由.
的值等于多少时.△PFD∽△BFP?并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com