
 .若球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为2.25米,
.若球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为2.25米,
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源:不详 题型:解答题

 时,求直线AN的解析式.
时,求直线AN的解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
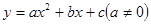 的图象如图所示, 其中对称轴为:x=1,则下列4个结论中正确的结论有( )个
的图象如图所示, 其中对称轴为:x=1,则下列4个结论中正确的结论有( )个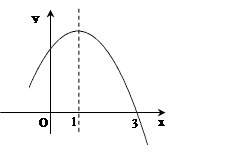
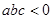 ; ②
; ② 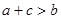 ;③
;③ 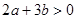 ; ④
; ④ 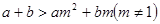 ;⑤
;⑤ 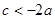 .
.| A.2个 | B.3个 | C.4个 | D.5个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
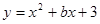 的图象经过点(3,0).
的图象经过点(3,0).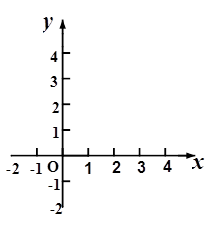
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ;②
;② ; ③
; ③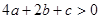 ;④
;④ ;⑤
;⑤
 其中正确的是( )
其中正确的是( )
| A.2个 | B.3个 | C.4个 | D.5 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
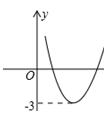
| A.无实数根 | B.有两个相等实数根 |
| C.有两个异号实数根 | D.有两个同号不等实数根 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com