
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y= (x>0)的函数图象经过点D,点P是一次函数
(x>0)的函数图象经过点D,点P是一次函数
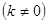 的图象与该反比例函数图象的一个公共点.
的图象与该反比例函数图象的一个公共点.
(1)求反比例函数的解析式;
(2)通过计算,说明一次函数
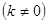 的图象一定过点C;
的图象一定过点C;
(3)对于一次函数
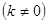 ,当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).
,当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).
(1) y= .(2)说明见解析;(3)
.(2)说明见解析;(3) <a<3.
<a<3.
解析试题分析:(1)求反比例函数的解析式,只需确定图象上一个点的坐;
(2)图象一定过点即点的坐标是解析式的解;
(3)一次函数y随x的增大而增大,即k>0.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD=BC.
∵B(3,1),C(3,3),
∴BC⊥x轴,AD=BC=2.
而A点坐标为(1,0),
∴点D的坐标为(1,2).
∵反比例函数y=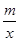 (x>0)的函数图象经过点D(1,2),
(x>0)的函数图象经过点D(1,2),
∴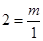 .
.
∴m=2
∴反比例函数的解析式为y= .
.
(2)当x=3时,y=kx+3-3k=3,
∴一次函数一次函数y=kx+3-3k(k≠0)的图象一定过点C.
(3)设点P的横坐标为a,则a的范围为 <a<3.
<a<3.
考点:1.平行四边形的性质;2.反比例函数;3.一次函数;4.点的坐标与函数解析式的关系.


科目:初中数学 来源: 题型:解答题
如图,已知反比例函数y= 与一次函数y=kx+b的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.
与一次函数y=kx+b的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.
(1)求反比例函数和一次函数的解析式;
(2)若点D的坐标为(1,0),求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,点D在直线上,D的横纵坐标之积为2,过D作两坐标轴的垂线DC、DE,连接OD.
(1)求证:AD平分∠CDE;
(2)对任意的实数b(b≠0),求证:AD•BD为定值;
(3)是否存在直线AB,使得四边形OBCD为平行四边形?若存在,求出直线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小明家距离学校8千米,今天早晨小明骑车上学途中,自行车突然“爆胎”,恰好路边有便民服务点,几分钟后车修好了,他加快速度骑车到校,我们根据小明的这段经历画了一幅图象,该图描绘了小明行驶路程s与所用时间t之间的函数关系,请根据图象回答下列问题:
(1)小明骑车行驶了多少千米时,自行车“爆胎”修车用了几分钟?
(2)小明共用多长时间到学校的?
(3)小明修车前的速度和修车后的速度分别是多少?
(4)如果自行车未“爆胎”,小明一直按修车前速度行驶,那么他比实际情况早到或晚到多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知一次函数图象如图:
(1)求一次函数的解析式;
(2)若点P为该一次函数图象上一点,且点A为该函数图象与x轴的交点,若S△PAO=6,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图象提供的信息,解答下列问题:
(1)求出蜡烛燃烧时y与x之间的函数关系式;
(2)求蜡烛从点燃到燃尽所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系 中,一次函数
中,一次函数 (a为常数)的图象与y轴相交于点A,与函数
(a为常数)的图象与y轴相交于点A,与函数 的图象相交于点B
的图象相交于点B ,
, .
.
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行)。下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.
(1)写出渔船离港口的距离S和它离开港口的时间t的函数关系式;
(2)在渔船返航途中,什么时间范围内两船间距离不超过30海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com