
分析 (1)方程去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去括号,移项合并,把x系数化为1,即可求出解;
(4)方程去括号,移项合并,把x系数化为1,即可求出解;
(5)方程去括号,移项合并,把x系数化为1,即可求出解;
(6)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)去括号得:5x+10=10x-2,
移项合并得:5x=12,
解得:x=2.4;
(2)去括号得:x+1-2x+2=1-3x,
移项合并得:2x=-2,
解得:x=-1;
(3)去括号得:3-2x-2=2x-6,
移项合并得:4x=7,
解得:x=1.75;
(4)去括号得:8x-4-15x-3=14,
移项合并得:-7x=21,
解得:x=-3;
(5)去括号得:4x+2=3x+6-x-6,
移项合并得:2x=-2,
解得:x=-1;
(6)去分母得:18(x+1)-2(x-1)=24(x-1)-21(x+1),
去括号得:18x+18-2x+2=24x-24-21x-21,
移项合并得:13x=-65,
解得:x=-5.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
 已知:如图,等腰△ABC中,AB=AC,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,点M、N分别为线段BO和CO中点.求证:四边形EDNM是矩形.
已知:如图,等腰△ABC中,AB=AC,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,点M、N分别为线段BO和CO中点.求证:四边形EDNM是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
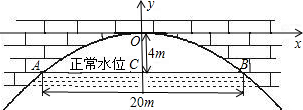 如图,有一抛物线形拱桥,正常水位时桥下水面宽20m,拱顶距离水面4m.已知其抛物线解析式为y=-0.04x2,在正常水位时,桥下的水深为2m,为保证过往船只顺利通行,桥下水面的宽度不得小于18m,求水深超过多少米时,就会影响过往船只从桥下顺利通行?
如图,有一抛物线形拱桥,正常水位时桥下水面宽20m,拱顶距离水面4m.已知其抛物线解析式为y=-0.04x2,在正常水位时,桥下的水深为2m,为保证过往船只顺利通行,桥下水面的宽度不得小于18m,求水深超过多少米时,就会影响过往船只从桥下顺利通行?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com