
 x+2与坐标轴交于A、B两点,与双曲线y=
x+2与坐标轴交于A、B两点,与双曲线y= 交于点C,A、D关于y轴对称,若S四边形OBCD=6,则k= .
交于点C,A、D关于y轴对称,若S四边形OBCD=6,则k= .

 x+2),根据已知得出S△ACD﹣S△AOB=6,推出
x+2),根据已知得出S△ACD﹣S△AOB=6,推出 ×(4+4)×(
×(4+4)×(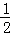 x+2)﹣
x+2)﹣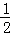 ×4×2=6,求出C的坐标即可.
×4×2=6,求出C的坐标即可.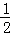 x+2,
x+2,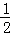 x+2,
x+2,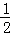 x+2上,
x+2上,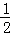 x+2),
x+2),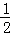 ×(4+4)×(
×(4+4)×(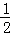 x+2)﹣
x+2)﹣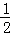 ×4×2=6,
×4×2=6,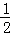 x+2=
x+2= ,
, ),
),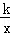 得:k=
得:k= .
. .
.

科目:初中数学 来源:不详 题型:解答题
 x与双曲线y=
x与双曲线y= 相交于A、B两点,BC⊥x轴于点C(﹣4,0).
相交于A、B两点,BC⊥x轴于点C(﹣4,0).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象相交于A,B两点,已知A(1,4).
的图象相交于A,B两点,已知A(1,4).
 的解集.
的解集.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 上,B、D在双曲线y2=
上,B、D在双曲线y2=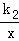 上,k1=2k2(k1>0),AB∥y轴,S?ABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,S?ABCD=24,则k1= .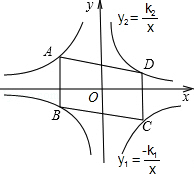
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 (x<0)的图象于B,交函数
(x<0)的图象于B,交函数 (x>0)的图象于C,则线段AB与线段AC的长度之比为 _________ .
(x>0)的图象于C,则线段AB与线段AC的长度之比为 _________ .
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
(x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com