练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

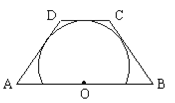
    【题目】如图，点在梯形的下底上，且与梯形的上底及两腰都相切，若，则梯形的周长等于 。

    【答案】

    【解析】

    由题意得DF=DE= HO =1，设半径为r，在Rt△AOE和Rt△DAH中，分别用勾股定理得到关于r和AE的式子，联立可消去r，解出AE的长，又由BG=AE，可求得梯形周长.

    解：

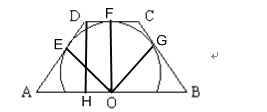
    如图所示：点E、F、G分别为切点，链接OE、OF、OG，过D作DH⊥AB于H，

    根据题意可知梯形为等腰梯形，，则DF=DE= HO =1，OA=2.5

    OF⊥CD，OE⊥AD，设圆的半径为r，

    在Rt△AOE中，由勾股定理得：，

    在Rt△DAH中，由勾股定理得：，

    整理可得：，解得AE=1.5cm（负值已舍去），

    ∴BG=AE=1.5cm，梯形的周长=AB+BG+GC+CD+DE+EA=12cm.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】有三张正面分别标有数字，2，4的不透明卡片，它们除数字外都相同；现将它们背面朝上，洗匀后，从三张卡片中随机地抽出一张，记住数字；

    若把抽出的卡片放回，洗匀后，再从三张卡片中随机抽出一张，记住数字试用列表或树状图的方法，求两次抽取的卡片上的数字为一正数、一负数的概率．

    若不把抽出的卡片放回，再从剩余两张卡片中随机抽出一张，直接写出两次抽取卡片上的数字为一正数、一负数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下表记录了一名球员在罚球线上投篮的结果，这么球员投篮一次，投中的概率约是( )

    投篮次数

    10

    50

    100

    150

    200

    250

    300

    500

    投中次数

    4

    35

    60

    78

    104

    123

    152

    251

    投中频率

    0.40

    0.70

    0.60

    0.52

    0.52

    0.49

    0.51

    0.50

    A. 0.7B. 0.6C. 0.5D. 0.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

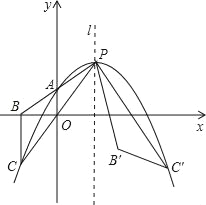
    【题目】如图，抛物线y＝a（x﹣m﹣1）2+2m（其中m＞0）与其对称轴l相交于点P．与y轴相交于点A（0，m）连接并延长PA、PO，与x轴、抛物线分别相交于点B、C，连接BC将△PBC绕点P逆时针旋转，使点C落在抛物线上，设点C、B的对应点分别是点B′和C′．

    （1）当m＝1时，该抛物线的解析式为：　 　．

    （2）求证：∠BCA＝∠CAO；

    （3）试问：BB′+BC﹣BC′是否存在最小值？若存在，求此时实数m的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

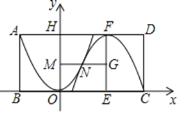
    【题目】超市有一种“喜之郎“果冻礼盒，内装两个上下倒置的果冻，果冻高为4cm，底面是个直径为6cm的圆，轴截面可以近似地看作一个抛物线，为了节省成本，包装应尽可能的小，这个包装盒的长不计重合部分，两个果冻之间没有挤压至少为　　

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y＝ax2+bx+c（a、b、c为常数，且a≠0）的图象如图所示，给出下列结论：①b2＞4ac； ②abc＜0；③a＜b； ④b+c＞3a；⑤方程ax2+bx+c＝0的两根之和的一半大于﹣1．其中，正确的结论有（　　）

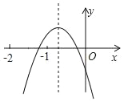
    A. ①②③⑤B. .①②④⑤C. ①②④D. .①②③④⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市实施产业精准扶贫，帮助贫困户承包荒山种植某品种蜜柚．已知该蜜柚的成本价为6元/千克，到了收获季节投入市场销售时，调查市场行情后，发现该蜜柚不会亏本，且每天的销售量y（千克）与销售单价x（元）之间的函数关系如图所示．

    （1）求y与x的函数关系式，并写出x的取值范围；

    （2）当该品种蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？

    （3）某村农户今年共采摘蜜柚12000千克，若该品种蜜柚的保质期为50天，按照（2）的销售方式，能否在保质期内全部销售完这批蜜柚？若能，请说明理由；若不能，应定销售价为多少元时，既能销售完又能获得最大利润？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

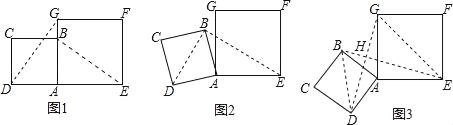
    【题目】在数学兴趣小组活动中，小明进行数学探究活动，将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置，AD与AE在同一直线上，AB与AG在同一直线上．

    （1）小明发现DG⊥BE，请你帮他说明理由．

    （2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长．

    （3）如图3，小明将正方形ABCD绕点A继续逆时针旋转，线段DG与线段BE将相交，交点为H，写出△GHE与△BHD面积之和的最大值，并简要说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

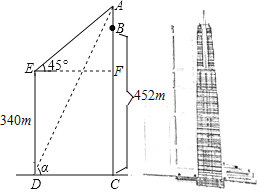
    【题目】如图，长沙九龙仓国际金融中心主楼BC高达452m，是目前湖南省第一高楼，和它处于同一水平面上的第二高楼DE高340m，为了测量高楼BC上发射塔AB的高度，在楼DE底端D点测得A的仰角为α，在顶端E点测得A的仰角∠AEF=45°，

    （1）若设AB为x米，请用含x的代数式表示AF的长．

    （2）求出发射塔AB的高度．（cosα≈，sinα≈，tanα≈）

    查看答案和解析>>

    同步练习册答案