
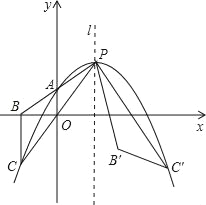
【题目】如图,抛物线y=a(x﹣m﹣1)2+2m(其中m>0)与其对称轴l相交于点P.与y轴相交于点A(0,m)连接并延长PA、PO,与x轴、抛物线分别相交于点B、C,连接BC将△PBC绕点P逆时针旋转,使点C落在抛物线上,设点C、B的对应点分别是点B′和C′.
(1)当m=1时,该抛物线的解析式为: .
(2)求证:∠BCA=∠CAO;
(3)试问:BB′+BC﹣BC′是否存在最小值?若存在,求此时实数m的值,若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+x+1;(2)见解析;(3)BB′+BC﹣BC′存在最小值,m=1+
x2+x+1;(2)见解析;(3)BB′+BC﹣BC′存在最小值,m=1+![]() .
.
【解析】
(1)把点A的坐标代入二次函数表达式得:m=a(﹣m﹣1)2+2m,解得:a=﹣![]() ,把m=1代入上式,即可求解;
,把m=1代入上式,即可求解;
(2)求出点B、C的坐标,即可求解;
(3)当点B′落在BC′所在的直线时,BB′+BC﹣BC′存在最小值,证△BAO∽△POD,即可求解.
解:(1)把点A的坐标代入二次函数表达式得:m=a(﹣m﹣1)2+2m,解得:a=﹣![]() ,
,
则二次函数的表达式为:y=﹣![]() (x﹣m﹣1)2+2m…①,
(x﹣m﹣1)2+2m…①,
则点P的坐标为(m+1,2m),点A的坐标为(0,m),
把m=1代入①式,整理得:y=﹣![]() x2+x+1,
x2+x+1,
故:答案为:y=﹣![]() x2+x+1;
x2+x+1;
(2)把点P、A的坐标代入一次函数表达式:y=kx+b得:
![]() ,解得:
,解得: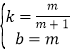 ,
,
则直线PA的表达式为:y=![]() x+m,
x+m,
令y=0,解得:x=﹣m﹣1,即点B坐标为(﹣m﹣1,0),
同理直线OP的表达式为:y=![]() x…②,
x…②,
将①②联立得:a(x﹣m﹣1)2+2m﹣![]() x=0,其中a=﹣
x=0,其中a=﹣![]() ,
,
该方程的常数项为:a(m+1)2+2m,
由韦达定理得:x1x2=xCxP=![]() =
=![]() =﹣(m+1)2,
=﹣(m+1)2,
其中
则xC=﹣m﹣1=xB,
∴BC∥y轴,
∴∠BCA=∠CAO;
(3)如图当点B′落在BC′所在的直线时,BB′+BC﹣BC′存在最小值,

设:直线l与x轴的交点为D点,连接BB′、CC′,
∵点C关于l的对称点为C′,
∴CC′⊥l,而OD⊥l,∴CC′∥OD,∴∠POD=∠PCC′,
∵∠PB′C′+∠PB′B=180°,
△PB′C′由△PBC旋转而得,
∴∠PBC=∠PB′C′,PB=PB′,∠BPB′=∠CPC′,
∴∠PBC+∠PB′B=180°,
∵BC∥AO,
∴∠ABC+∠BAO=180°,
∴∠PB′B=∠BAO,
∵PB=PB′,PC=PC′,
∴∠PB′B=∠PBB′=![]() ,
,
∴∠PCC′=∠PC′C=![]() ,
,
∴∠PB′B=∠PCC′,
∴∠BAO=∠PCC′,
而∠POD=∠PCC′,
∴∠BAO=∠POD,
而∠POD=∠BAO=90°,
∴△BAO∽△POD,
∴![]() ,
,
将BO=m+1,PD=2m,AO=m,OD=m+1代入上式并解得:
m=1+![]() (负值已舍去).
(负值已舍去).


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
(1)求抛物线的函数表达式;
(2)根据图像,直接写出不等式x2+bx+c>0的解集: .
(3)设D为抛物线上一点,E为对称轴上一点,若以点A,B,D,E为顶点的四边形是菱形,则点D的坐标为: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),其表达式是y=ax2+c的形式.请根据所给的数据求出a,c的值.
(2)求支柱MN的长度.
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.

(1)如图1,若CE=CF,求证:DE=DF;
(2)如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
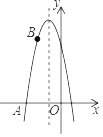
【题目】已知抛物线的对称轴是直线x=﹣1,与x轴一个交点是点A(﹣3,0),且经过点B(﹣2,6)
(1)求该抛物线的解析式;
(2)若点(﹣![]() ,y1)与点(2,y2)都在该抛物线上,直接写出y1与y2的大小关系.
,y1)与点(2,y2)都在该抛物线上,直接写出y1与y2的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
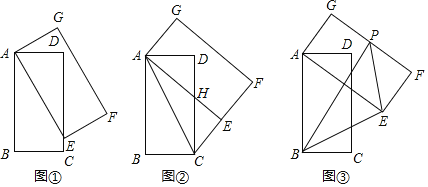
【题目】在矩形ABCD中,![]() ,
,![]() ,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为
,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为![]() ,得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.
,得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.
![]() 如图
如图![]() ,当点E落在DC边上时,直写出线段EC的长度为______;
,当点E落在DC边上时,直写出线段EC的长度为______;
![]() 如图
如图![]() ,当点E落在线段CF上时,AE与DC相交于点H,连接AC,
,当点E落在线段CF上时,AE与DC相交于点H,连接AC,
![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 直接写出线段DH的长度为______.
直接写出线段DH的长度为______.
![]() 如图
如图![]() 设点P为边FG的中点,连接PB,PE,在矩形ABCD旋转过程中,
设点P为边FG的中点,连接PB,PE,在矩形ABCD旋转过程中,![]() 的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“垃圾分一分,明天美十分”.环保部门计划订制一批垃圾分类宣传海报,海报版面不小于300平方米,当宣传海报的版面为300平方米时,价格为80元/平方米.为了支持垃圾分类促进环保,广告公司给予以下优惠:宣传海报版面每增加1平方米,每平方米的价格减少0.2元,但不能低于50元/平方米.假设宣传海报的版面增加![]() 平方米后,总费用为
平方米后,总费用为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)订制宣传海报的版面为多少平方米时总费用最高?最高费用为多少元?
(3)环保部门希望总费用尽可能低,那么应该订制多少平方米的海报?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,使得C′C∥AB,则∠CAB'等于( )
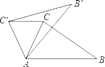
A. 30°B. 25°C. 15°D. 10°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com