
����Ŀ����������۸��߸ߣ������������������ĸ߶ȹ�ע�����г������ƽ���۸�ÿǧ�˴ﵽһ���ĵ���ʱ��������Ͷ�봢��������ƽ������۸�
��1���ӽ��������5��20�գ�����۸��߸ߣ�5��20�ձ�����۸�������60%��ij�����ڽ���5��20�չ���2.5ǧ����������Ҫ��100ԪǮ����ô��������������ͼ۸�Ϊÿǧ�˶���Ԫ��
��2��5��20�գ�����۸�Ϊÿǧ��40Ԫ.5��21�գ�ij�о���Ͷ�봢�����Ⲣ�涨�����ۼ���ÿǧ��40Ԫ�Ļ������µ�a%���ۣ�ij���а��涨�۳���һ���������⣬�ó����ڷǴ�������ļ۸���Ϊÿǧ��40Ԫ������£����������������������5��20��������a%���Ҵ������������ռ�������� ![]() �������������۵��ܽ���5��20�������
�������������۵��ܽ���5��20������� ![]() a%����a��ֵ��
a%����a��ֵ��
���𰸡�
��1��
�⣺������������۸�Ϊÿǧ��xԪ��
��������ã�2.5����1+60%��x��100��
��ã�x��25��
�𣺽�������������ͼ۸�Ϊÿǧ��25Ԫ
��2��
�⣺��5��20����������������Ϊ1��
��������ã�40��1��a%���� ![]() ��1+a%��+40��
��1+a%��+40�� ![]() ��1+a%��=40��1+
��1+a%��=40��1+ ![]() a%����
a%����
��a%=y��ԭ���̻�Ϊ��40��1��y���� ![]() ��1+y��+40��
��1+y��+40�� ![]() ��1+y��=40��1+
��1+y��=40��1+ ![]() y����
y����
�����ã�5y2��y=0��
��ã�y=0.2����y=0����ȥ����
��a%=0.2��
��a=20��
��a��ֵΪ20
����������1��������������۸�Ϊÿǧ��xԪ�����������г�һԪһ�β���ʽ���ⲻ��ʽ���ɣ���2����5��20����������������Ϊ1�����������г����̣��ⷽ�̼��ɣ����⿼����һԪһ�β���ʽ��Ӧ�á�һԪ���η��̵�Ӧ�ã����������г�����ʽ�ͷ����ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ��Լˮ��Դ���ƶ����µľ�����ˮ�շѱ��������±����û�ÿ�½��ɵ�ˮ��y��Ԫ����ÿ����ˮ��x��m3��֮��Ĺ�ϵ��ͼ��ʾ��
��1����y����x�ĺ�������ʽ��
��2����ij�û��������·ݹ���ˮ40m3�����·���ˮ��������25m3��������ˮ��79.8Ԫ������û��������·ݵ���ˮ�����Ƕ���m3��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣺![]() ��4sin30��+��2015���У�0������3��2
��4sin30��+��2015����0������3��2
��2���Ȼ�������ֵ��1��![]() ��
��![]() ������x��y����|x��2|+��2x��y��3��2=0��
������x��y����|x��2|+��2x��y��3��2=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
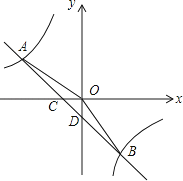
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ�����ͼ���뷴����������ͼ���ڵڶ����������ڵ�A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D����B�������ǣ�m����4��������AO��AO=5��sin��AOC= ![]() ��
��
��1�����������Ľ���ʽ��
��2������OB�����AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������ֱ�ߵ�·��ͬ��㡢ͬ�յ㡢ͬ���ֱ��Բ�ͬ���ٶ������ܲ�1500�ף��ȵ��յ����ԭ����Ϣ����֪���ȳ���30����Ҳų��������ܲ������������У��ס������˵ľ���y���ף���׳�����ʱ��x���룩֮��Ĺ�ϵ��ͼ��ʾ�����ҵ��յ�ʱ�����յ�ľ������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=10��AC=8��BC=6���Ա�AB���е�OΪԲ�ģ�����Բ��AC���У���P��Q�ֱ��DZ�BC�Ͱ�Բ�ϵĶ��㣬����PQ����PQ�������ֵ����Сֵ�ĺ��ǣ�������
A.6
B.2 ![]() +1
+1
C.9
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˱���������ѧУ��չ��ȫУ�Ե�������������ǰ�������ȡ����ѧ����������ǵ������������ͼ��ʾ�����ݰ�����˵㲻�����Ҷ˵㣬��ȷ��0.1��������ٴμ���ⲿ��ѧ������������������ʾ��
���� | Ƶ�� |
4.0��x��4.2 | 2 |
4.2��x��4.4 | 3 |
4.4��x��4.6 | 5 |
4.6��x��4.8 | 8 |
4.8��x��5.0 | 17 |
5.0��x��5.2 | 5 |

��1��������ȡ��ѧ��������
��2���������ﵽ4.8������Ϊ��꣬���ƻǰ��Уѧ������������ʣ�
��3����ѡ���ʵ���ͳ��������������ͬ�ĽǶȷ����ǰ��������ݣ������������������Ч����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c���������Ҿ����㣨1��1����˫����y= ![]() �����㣨a��bc�����������н��ۣ���bc��0����b+c��0����b��c�ǹ���x��һԪ���η���x2+��a��1��x+
�����㣨a��bc�����������н��ۣ���bc��0����b+c��0����b��c�ǹ���x��һԪ���η���x2+��a��1��x+ ![]() =0������ʵ��������a��b��c��3��������ȷ����������д��ţ�
=0������ʵ��������a��b��c��3��������ȷ����������д��ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ک�2����1��0��1��2�����������ȡ����m��n������κ���y=��x��m��2+n�Ķ������������ϵĸ���Ϊ��������
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com