
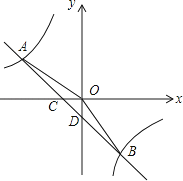
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC= ![]() .
.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
【答案】
(1)
解:过点A作AE⊥x轴于点E,如图所示.
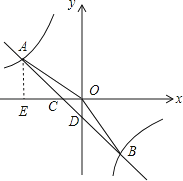
设反比例函数解析式为y= ![]() .
.
∵AE⊥x轴,
∴∠AEO=90°.
在Rt△AEO中,AO=5,sin∠AOC= ![]() ,∠AEO=90°,
,∠AEO=90°,
∴AE=AOsin∠AOC=3,OE= ![]() =4,
=4,
∴点A的坐标为(﹣4,3).
∵点A(﹣4,3)在反比例函数y= ![]() 的图象上,
的图象上,
∴3= ![]() ,解得:k=﹣12.
,解得:k=﹣12.
∴反比例函数解析式为y=﹣ ![]() .
.
(2)
解:∵点B(m,﹣4)在反比例函数y=﹣ ![]() 的图象上,
的图象上,
∴﹣4=﹣ ![]() ,解得:m=3,
,解得:m=3,
∴点B的坐标为(3,﹣4).
设直线AB的解析式为y=ax+b,
将点A(﹣4,3)、点B(3,﹣4)代入y=ax+b中得:
![]() ,解得:
,解得: ![]() ,
,
∴一次函数解析式为y=﹣x﹣1.
令一次函数y=﹣x﹣1中y=0,则0=﹣x﹣1,
解得:x=﹣1,即点C的坐标为(﹣1,0).
S△AOB= ![]() OC(yA﹣yB)=
OC(yA﹣yB)= ![]() ×1×[3﹣(﹣4)]=
×1×[3﹣(﹣4)]= ![]()
【解析】(1)过点A作AE⊥x轴于点E,设反比例函数解析式为y= ![]() .通过解直角三角形求出线段AE、OE的长度,即求出点A的坐标,再由点A的坐标利用待定系数法求出反比例函数解析式即可;(2)由点B在反比例函数图象上可求出点B的坐标,设直线AB的解析式为y=ax+b,由点A、B的坐标利用待定系数法求出直线AB的解析式,令该解析式中y=0即可求出点C的坐标,再利用三角形的面积公式即可得出结论.本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式以及三角形的面积公式,解题的关键是:(1)求出点A的坐标;(2)求出直线AB的解析式.本题属于基础题,难度不大,解决该题型题目时,根据点的坐标利用待定系数法求出函数解析式是关键.
.通过解直角三角形求出线段AE、OE的长度,即求出点A的坐标,再由点A的坐标利用待定系数法求出反比例函数解析式即可;(2)由点B在反比例函数图象上可求出点B的坐标,设直线AB的解析式为y=ax+b,由点A、B的坐标利用待定系数法求出直线AB的解析式,令该解析式中y=0即可求出点C的坐标,再利用三角形的面积公式即可得出结论.本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式以及三角形的面积公式,解题的关键是:(1)求出点A的坐标;(2)求出直线AB的解析式.本题属于基础题,难度不大,解决该题型题目时,根据点的坐标利用待定系数法求出函数解析式是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
①BE=CD;
②∠DGF=135°;
③∠ABG+∠ADG=180°;
④若![]() =
=![]() ,则3S△BDG=13S△DGF .
,则3S△BDG=13S△DGF .
其中正确的结论是 写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,﹣2),反比例函数y=![]() 的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
(1)求反比例函数与一次函数的解析式;
(2)求反比例函数与一次函数的另一个交点M的坐标;
(3)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P的坐标是(a,b),从﹣2,﹣1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )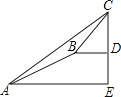
A.8.1米
B.17.2米
C.19.7米
D.25.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%.某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)5月20日,猪肉价格为每千克40元.5月21日,某市决定投入储备猪肉并规定其销售价在每千克40元的基础上下调a%出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的 ![]() ,两种猪肉销售的总金额比5月20日提高了
,两种猪肉销售的总金额比5月20日提高了 ![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+b与反比例函数y= ![]() (x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
(x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
(1)b=(用含m的代数式表示);
(2)若S△OAF+S四边形EFBC=4,则m的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com