
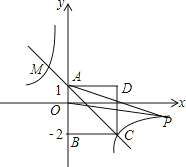
【题目】如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,﹣2),反比例函数y=![]() 的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
(1)求反比例函数与一次函数的解析式;
(2)求反比例函数与一次函数的另一个交点M的坐标;
(3)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
【答案】
(1)
解:(1)∵点A的坐标为(0,1),点B的坐标为(0,﹣2),
∴AB=1+2=3,
∵四边形ABCD为正方形,
∴Bc=3,
∴C(3,﹣2),
把C(3,﹣2)代入y=![]() 得k=3×(﹣2)=﹣6,
得k=3×(﹣2)=﹣6,
∴反比例函数解析式为y=﹣![]() ,
,
把C(3,﹣2),A(0,1)代入y=ax+b得![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y=﹣x+1
(2)
解:解方程组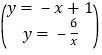 得
得![]() 或
或![]() ,
,
∴M点的坐标为(﹣2,3);
(3)
解:
设P(t,﹣![]() ),
),
∵△OAP的面积恰好等于正方形ABCD的面积,
∴![]() ×1×|t|=3×3,解得t=18或t=﹣18,
×1×|t|=3×3,解得t=18或t=﹣18,
∴P点坐标为(18,﹣![]() )或(﹣18,
)或(﹣18,![]() )
)
【解析】(1)先根据A点和B点坐标得到正方形的边长,则BC=3,于是可得到C(3,﹣2),然后利用待定系数法求反比例函数与一次函数的解析式;
(2)通过解关于反比例函数解析式与一次函数的解析式所组成的方程组可得到M点的坐标;
(3)设P(t,﹣![]() ),根据三角形面积公式和正方形面积公式得到
),根据三角形面积公式和正方形面积公式得到![]() ×1×|t|=3×3,然后解绝对值方程求出t即可得到P点坐标.
×1×|t|=3×3,然后解绝对值方程求出t即可得到P点坐标.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线l1经过原点与A点,其顶点是P(﹣2,3),平行于y轴的直线m与x轴交于点B(b,0),与抛物线l1交于点M.
(1)点A的坐标是;抛物线l1的解析式是;
(2)当BM=3时,求b的值;
(3)把抛物线l1绕点(0,1)旋转180°,得到抛物线l2 .
①直接写出当两条抛物线对应的函数值y都随着x的增大而减小时,x的取值范围;
(4)②直线m与抛物线l2交于点N,设线段MN的长为n,求n与b的关系式,并求出线段MN的最小值与此时b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).
(1)求线段CD的长。
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
(3)伴随P,Q两点的运动,线段PQ的垂直平分线为l.
①t为何值时,l经过点C?
②求当l经过点D时t的值,并求出此时刻线段PQ的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:![]() ﹣4sin30°+(2015﹣π)0﹣(﹣3)2
﹣4sin30°+(2015﹣π)0﹣(﹣3)2
(2)先化简,再求值:1﹣![]() ÷
÷![]() ,其中x、y满足|x﹣2|+(2x﹣y﹣3)2=0.
,其中x、y满足|x﹣2|+(2x﹣y﹣3)2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ![]() ,则大楼AB的高度约为( )(精确到0.1米,参考数据:
,则大楼AB的高度约为( )(精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,
≈1.73, ![]() ≈2.45)
≈2.45)
A.30.6
B.32.1
C.37.9
D.39.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC= ![]() .
.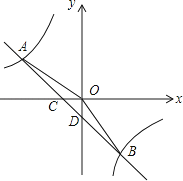
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
A.6
B.2 ![]() +1
+1
C.9
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,∠ABC=45°,AH⊥BC于点H,点D在AH上,且DH=CH,连结BD.
(1)求证:BD=AC;
(2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应),连接AE.
①如图②,当点F落在AC上时,(F不与C重合),若BC=4,tanC=3,求AE的长;
②如图③,当△EHF是由△BHD绕点H逆时针旋转30°得到时,设射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com