
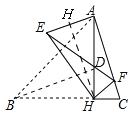
����Ŀ����ͼ�٣���ABC�У���ABC=45�㣬AH��BC�ڵ�H����D��AH�ϣ���DH=CH������BD��
��1����֤��BD=AC��
��2������BHD�Ƶ�H��ת���õ���EHF����B��D�ֱ����E��F��Ӧ��������AE��
����ͼ�ڣ�����F����AC��ʱ����F����C�غϣ�����BC=4��tanC=3����AE�ij���
����ͼ�ۣ�����EHF���ɡ�BHD�Ƶ�H��ʱ����ת30��õ�ʱ��������CF��AE�ཻ�ڵ�G������GH����̽���߶�GH��EF֮������ĵ�����ϵ����˵�����ɣ�
���𰸡�
��1��
֤������Rt��AHB�У���ABC=45�㣬
��AH=BH��
�ڡ�BHD�͡�AHC�У�
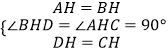 ��
��
���BHD�ա�AHC��
��BD=AC��
��2��
�⣺����ͼ��
��Rt��AHC��
��tanC=3��
�� ![]() =3��
=3��
��CH=x��
��BH=AH=3x��
��BC=4��
��3x+x=4��
��x=1��
��AH=3��CH=1��
����ת֪����EHF=��BHD=��AHC=90�㣬EH=AH=3��CH=DH=FH��
���EHA=��FHC�� ![]() ��
��
���EHA�ա�FHC��
���EAH=��C��
��tan��EAH=tanC=3��
����H��HP��AE��
��HP=3AP��AE=2AP��
��Rt��AHP��AP2+HP2=AH2��
��AP2+��3AP��2=9��
��AP= ![]() ��
��
��AE= ![]() ��
��
���ɢ��У���AEH�͡�FHC��Ϊ���������Σ�
���GAH=��HCG=90�㣬
���AGQ�ס�CHQ��
�� ![]() ��
��
�� ![]() ��
��
�ߡ�AQC=��GQE��
���AQC�ס�GQH��
�� ![]() =sin30��=
=sin30��= ![]()
����������1�����жϳ�AH=BH�����жϳ���BHD�ա�AHC���ɣ���2�����ȸ���tanC=3�����AH=3��CH=1��Ȼ����ݡ�EHA�ա�FHC���õ���HP=3AP��AE=2AP������ù��ɶ������ɣ������жϳ���AGQ�ס�CHQ���õ� ![]() ��Ȼ���жϳ���AQC�ס�GQH�������Ʊȼ��ɣ������Ǽ��α任�ۺ��⣬��Ҫ��������ת�����ʣ�ȫ�������ε����ʺ��ж������������ε����ʺ��ж������ɶ�����������Ǻ��������壬���������ε��ж������ʣ��Ȿ��Ĺؼ����������������ʺ��ж������ã�
��Ȼ���жϳ���AQC�ס�GQH�������Ʊȼ��ɣ������Ǽ��α任�ۺ��⣬��Ҫ��������ת�����ʣ�ȫ�������ε����ʺ��ж������������ε����ʺ��ж������ɶ�����������Ǻ��������壬���������ε��ж������ʣ��Ȿ��Ĺؼ����������������ʺ��ж������ã�
�����㾫����ͨ��������ù��ɶ����ĸ�������������ε��ж������ʣ�����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2�����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ�������Խ����⣮


 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪ�����Σ���A������Ϊ��0��1������B������Ϊ��0����2��������������y=![]() ��ͼ����C��һ�κ���y=ax+b��ͼ��A��C����.
��ͼ����C��һ�κ���y=ax+b��ͼ��A��C����.
��1������������һ�κ����Ľ���ʽ;
��2������������һ�κ�������һ������M������;
��3������P�Ƿ���������ͼ���ϵ�һ�㣬��OAP�����ǡ�õ���������ABCD���������P�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��x+b�뷴��������y= ![]() ��x��0����ͼ����A��B���㣬��x�ᡢy��ֱ���C��D���㣬����OA��OB����A��AE��x���ڵ�E����OB�ڵ�F�����A�ĺ�����Ϊm��
��x��0����ͼ����A��B���㣬��x�ᡢy��ֱ���C��D���㣬����OA��OB����A��AE��x���ڵ�E����OB�ڵ�F�����A�ĺ�����Ϊm��
��1��b=���ú�m�Ĵ���ʽ��ʾ����
��2����S��OAF+S�ı���EFBC=4����m��ֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y= ![]() x+2��˫�����ཻ�ڵ�A��m��3������x�ύ�ڵ�C��
x+2��˫�����ཻ�ڵ�A��m��3������x�ύ�ڵ�C��
��1����˫���߽���ʽ��
��2����P��x���ϣ������ACP�����Ϊ3�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017����ʡ�����У���25�⣬10�֣�����������ͼ1��P��ƽ��ֱ������ϵ��һ�㣨x���ϵĵ���⣩������P��PC��x���ڵ�C����C�Ƶ�P��ʱ����ת60���õ���Q�������ǽ����ɵ�P�õ���Q�IJ�����Ϊ���T�任��

��1����P��a��b������T�任��õ��ĵ�Q������Ϊ ������M����T�任��õ���N��6��![]() �������M������Ϊ ��
�������M������Ϊ ��
��2��A�Ǻ���![]() ͼ��������ԭ��O������һ�㣬����T�任��õ���B��
ͼ��������ԭ��O������һ�㣬����T�任��õ���B��
������O����B��ֱ�ߵĺ�������ʽ��
����ͼ2��ֱ��AB��y���ڵ�D������OAB���������OAD�����֮�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ű��ΪA��B��C��D�Ŀ�Ƭ��������⣬������ȫ��ͬ��������ֱ�д����ͼ��ʾ���������泯�ϣ�ϴ�ȷźã��ִ��������ȡһ�ţ����Żأ����ٴ�ʣ�µĿ�Ƭ�������ȡһ�ţ�
��1��������״ͼ���б��ķ�����ʾ���γ�ȡ��Ƭ�����п��ܳ��ֵĽ������Ƭ��A��B��C��D��ʾ����
��2������֪��������a2+b2=c2������������a��b��c��Ϊ����������鵽�����ſ�Ƭ�ϵ������ǹ������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�ı߳�Ϊ4����PΪBC���ϵ�����һ�㣨�����B��C�غϣ����ҡ�APD=60�㣬PD��AB�ڵ�D����BP=x��BD=y����y����x�ĺ���ͼ������ǣ�������
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���г���˾����������ѧѧ�������Ʒ���˽�����������ȡ����ѧ�������ʾ�������֡��dz��˽⡱�����Ƚ��˽⡱����һ���˽⡱�������˽⡱�������ͣ��ֱ��ΪA��B��C��D�����ݵ����������������в�������ͳ��ͼ��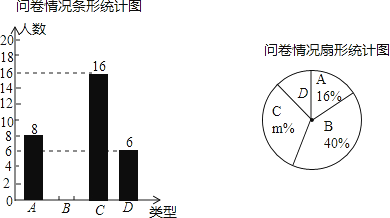
��1�������ʾ��������������ѧ��������ͳ��ͼ��m= ��
��2�������������Ϣ��ȫ����ͳ��ͼ��
��3������У��1000��ѧ��������ѡ�dz��˽⡱�����Ƚ��˽⡱��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com