
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).
(1)求线段CD的长。
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
(3)伴随P,Q两点的运动,线段PQ的垂直平分线为l.
①t为何值时,l经过点C?
②求当l经过点D时t的值,并求出此时刻线段PQ的长。
【答案】
(1)
解:如图1,作DE⊥BC于E,
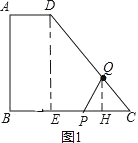
∵AD∥BC,∠A=90°,
∴四边形ABED为矩形,
∴BE=AD=1,DE=AB=3,
∴EC=BC﹣BE=4,
在Rt△DEC中,DE2+EC2=DC2,
∴CD=![]() =5厘米;
=5厘米;
(2)
解:∵点P的速度为1厘米/秒,点Q的速度为2厘米/秒,运动时间为t秒,
∴BP=t厘米,PC=(5﹣t)厘米,CQ=2t厘米,QD=(5﹣2t)厘米,
且0<t≤2.5,
作QH⊥BC于点H,
∴DE∥QH,
∴∠DEC=∠QHC,
∵∠C=∠C,
∴△DEC∽△QHC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴QH=![]() t,
t,
∴![]() =
=![]() =
=![]() (5-t)
(5-t)![]() =-
=-![]() ,
,
S四边形ABCD=![]() (AD+BC)
(AD+BC)![]() AB=
AB=![]() (1+5)×3=9,
(1+5)×3=9,
分两种情况讨论:
①当S△PQC:S四边形ABCD=1:3时,-![]() ,
,
即t2﹣5t+5=0,
解得:t1=![]() ,t2=
,t2=![]() (舍去);
(舍去);
②S△PQC:S四边形ABCD=2:3时,-![]() ,
,
即t2﹣5t+10=0,
∵△<0,
∴方程无解,
∴当t为![]() 秒时,线段PQ将四边形ABCD的面积分为1:2两部分;
秒时,线段PQ将四边形ABCD的面积分为1:2两部分;
(3)
解:如图2,

①当PQ的垂直平分线l经过点C时,可知PC=QC,
∴5﹣t=2t,
∴3t=5,
∴t=![]() ,
,
∴当t=![]() 秒时,直线l经过点C
秒时,直线l经过点C
②如图3,
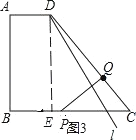
当PQ的垂直平分线l经过点D时,
可知DQ=DP,
连接DP,则在Rt△DEP中,DP2=DE2+EP2,
∴DQ2=DE2+EP2,
∴(5﹣2t)2=32+(t﹣1)2,
∴t1=1,t2=5(舍去),
∴BP=1厘米,
∴当t=1秒时,直线l经过点D,此时点P与点E重合;
如图4,连接FQ,
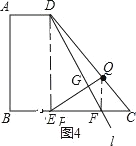
∵直线l是△DPQ的对称轴,
∴△DEF≌△DQF,∠DQF=90°,EF=QF,
设EF=x厘米,则QF=x厘米,FC=(4﹣x)厘米,
在Rt△FQC中,FQ2+QC2=FC2,
x2+22=(4﹣x)2,
∴x=![]() ,
,
∴EF=![]() 厘米,
厘米,
在Rt△DEF中,DE2+EF2=DF2,
∴32+(![]() )2=DF2,
)2=DF2,
∴DF=![]() 厘米,
厘米,
在Rt△DEF中,EG⊥DF,
∴![]() =
=![]()
![]() =
=![]()
![]() ,
,
∴EG=![]() ,
,
∴EG=![]() 厘米,
厘米,
∴PQ=2EG=![]() 厘米.
厘米.
【解析】(1)作DE⊥BC于E,根据勾股定理即可求解;
(2)线段PQ将四边形ABCD的面积分为1:2两部分,分两种情况进行求解;
(3)①当PQ的垂直平分线经过点C进行分析解答;
②当PQ的垂直平分线l经过点D时进行分析解答.
此题考查了梯形中动点问题,用到了勾股定理,垂直平分线定理等,注意分情况讨论。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在如图所示的二次函数y=ax2+bx+c的图象中,大伟同学观察后得出了以下四条结论:①a<0,b>0,c>0;②b2﹣4ac=0;③ ![]() <c;④关于x的一元二次方程ax2+bx+c=0有一个正根,你认为其中正确的结论有( )
<c;④关于x的一元二次方程ax2+bx+c=0有一个正根,你认为其中正确的结论有( ) 
A.1条
B.2条
C.3条
D.4条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为m的正方形面积为12,则下列关于m的说法中,错误的是( )
①m是无理数; ②m是方程m2﹣12=0的解; ③m满足不等式组![]() ; ④m是12的算术平方根
; ④m是12的算术平方根
A.①②
B.①③
C.③
D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师家距学校1900米,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23分钟,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20分钟,且骑电瓶车的平均速度是步行速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4分钟.
(1)求李老师步行的平均速度;
(2)请你判断李老师能否按时上班,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
①BE=CD;
②∠DGF=135°;
③∠ABG+∠ADG=180°;
④若![]() =
=![]() ,则3S△BDG=13S△DGF .
,则3S△BDG=13S△DGF .
其中正确的结论是 写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E为矩形ABCD边AD上的一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是2cm/s.若P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t的函数关系图象如图2,则下列结论错误的是( )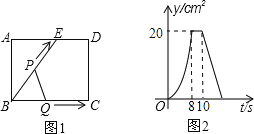
A.AE=12cm
B.sin∠EBC=![]()
C.当0<t≤8时,y=![]() t2
t2
D.当t=9s时,△PBQ是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,﹣2),反比例函数y=![]() 的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
(1)求反比例函数与一次函数的解析式;
(2)求反比例函数与一次函数的另一个交点M的坐标;
(3)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )
A.8.1米
B.17.2米
C.19.7米
D.25.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x+2与双曲线相交于点A(m,3),与x轴交于点C.
x+2与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com