
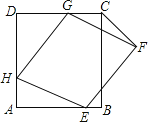
【题目】如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
【答案】详见解析
【解析】
试题分析:(1)连接GE,根据正方形的性质和平行线的性质得到∠AEG=∠CGE,根据菱形的性质和平行线的性质得到∠HEG=∠FGE,解答即可;
(2)证明Rt△HAE≌Rt△GDH,得到∠AHE=∠DGH,证明∠GHE=90°,根据正方形的判定定理证明.
证明:(1)连接GE,
∵AB∥CD,
∴∠AEG=∠CGE,
∵GF∥HE,
∴∠HEG=∠FGE,
∴∠HEA=∠CGF;
(2)∵四边形ABCD是正方形,
∴∠D=∠A=90°,
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△HAE和Rt△GDH中,
![]() ,
,
∴Rt△HAE≌Rt△GDH(HL),
∴∠AHE=∠DGH,又∠DHG+∠DGH=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴菱形EFGH为正方形;



 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】已知样本数据x1 , x2 , x3 , …,xn的方差为4,则数据2x1+3,2x2+3,2x3+3,…,2xn+3的方差为( )
A.11
B.9
C.16
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
①1是绝对值最小的数;
②0既不是正数,也不是负数;
③一个有理数不是整数就是分数;
④0的绝对值是0.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E。

(1)求证:AB=BE;
(2)若PA=2 ,cosB=![]() ,求⊙O半径的长。
,求⊙O半径的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com