
【题目】用适当的方法解下列方程.
(1)(6x-1)2-25=0; (2)(3x-2)2=x2;
(3)x2+![]() =
=![]() x; (4)(x+1)(x-1)+2(x+3)=8.
x; (4)(x+1)(x-1)+2(x+3)=8.
【答案】(1)x1=1,x2=-![]() ;(2)x1=1,x2=
;(2)x1=1,x2=![]() ;(3)x1=x2=
;(3)x1=x2=![]() ;(4)x1=-3,x2=1.
;(4)x1=-3,x2=1.
【解析】
(1)方程利用直接开平方法即可求出解;
(2)方程利用直接开平方法即可求出解;
(3)方程利用配方法即可求出解;
(4)方程利用因式分解法即可求出解.
解:(1)(6x-1)2-25=0
(6x-1)2=25
6x-1=±5
6x-1=5或6x-1=-5
∴![]() =1,
=1,![]() =-
=-![]() .
.
(2) (3x-2)2=x2
3x-2=±2
所以![]() =1,
=1,![]() =
=![]() .
.
(3)x2+![]() =
=![]() x
x
x2-![]() x+
x+![]() =0
=0
8 x2-![]() +1=0
+1=0
∴![]() =1,
=1,![]() =
=![]() .
.
(4)(x+1)(x1)+2(x+3)=8,
整理得:x21+2x+68=0,
即x2+2x3=0,
分解因式得:(x+3)(x1)=0,
可得x+3=0或x1=0,
解得:![]() =3,
=3, ![]() =1.
=1.


科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式的化简后,遇到了这样一个需要化简的式子:![]() .该如何化简呢?思考后,他发现3+2
.该如何化简呢?思考后,他发现3+2![]() =1+2
=1+2![]() +(
+(![]() )2=(1+
)2=(1+![]() )2.于是
)2.于是![]() =
=![]() =1+
=1+![]() .善于思考的小明继续深入探索;当a+b
.善于思考的小明继续深入探索;当a+b![]() =(m+n
=(m+n![]() )2时(其中a,b,m,n均为正整数),则a+b
)2时(其中a,b,m,n均为正整数),则a+b![]() =m2+2
=m2+2![]() mn+2n2.此时,a=m2+2n2,b=2mn,于是,
mn+2n2.此时,a=m2+2n2,b=2mn,于是,![]() =m+n
=m+n![]() .请你仿照小明的方法探索并解决下列问题:
.请你仿照小明的方法探索并解决下列问题:
(1)设a,b,m,n均为正整数且![]() =m+n
=m+n![]() ,用含m,n的式子分别表示a,b时,结果是a= ,b= ;
,用含m,n的式子分别表示a,b时,结果是a= ,b= ;
(2)利用(1)中的结论,选择一组正整数填空:![]() = +
= + ![]() ;
;
(3)化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2,且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
(1)当参加老师的人数为多少时,两家旅行社收费相同?
(2)求出y1、y2关于x的函数关系式?
(3)如果共有50人参加时,选择哪家旅行社合算?

查看答案和解析>>
科目:初中数学 来源: 题型:
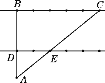
【题目】如图,一条河的两岸BC与DE互相平行,两岸各有一排景观灯(图中黑点代表景观灯),每排相邻两景观灯的间隔都是10 m,在与河岸DE的距离为16 m的A处(AD⊥DE)看对岸BC,看到对岸BC上的两个景观灯的灯杆恰好被河岸DE上两个景观灯的灯杆遮住.河岸DE上的两个景观灯之间有1个景观灯,河岸BC上被遮住的两个景观灯之间有4个景观灯,求这条河的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分.而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的6位数密码就很有必要了.有一种用“因式分解法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:x3+2x2﹣x﹣2因式分解的结果为(x﹣1)(x+1)(x+2),当x=18时,x﹣1=17,x+1=19,x+2=20,此时可以得到数字密码171920.
(1)根据上述方法,当x=21,y=7时,对于多项式x3﹣xy2分解因式后可以形成哪些数字密码?(写出两个)
(2)若多项式x3+(m﹣3n)x2﹣nx﹣21因式分解后,利用本题的方法,当x=27时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
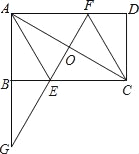
【题目】如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB至G,使BG=AB,连接GO交BC于E,延长GO交AD于F,连接AE.
求证:(1)△ABC≌△AOG;
(2)猜测四边形AECF的形状并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com