
【题目】矩形ABCD中,AD=8cm,AB=6cm,动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动,E点运动到B点停止,F点继续运动,运动到点D停止.如图可得到矩形CFHE,设F点运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是如图中的( )
A.
B.
C.
D.
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD. 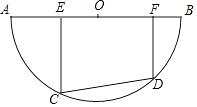
(1)求证:EO=OF;
(2)联结OC,如果△ECO中有一个内角等于45°,求线段EF的长;
(3)当动弦CD在弧AB上滑动时,设变量CE=x,四边形CDFE面积为S,周长为l,问:S与l是否分别随着x的变化而变化?试用所学的函数知识直接写出它们的函数解析式及函数定义域,以说明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P1、P2是反比例函数y= ![]() (k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点. 
(1)求反比例函数的解析式.
(2)①求P2的坐标. ②根据图象直接写出在第一象限内当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数y= ![]() 的函数值.
的函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在直角坐标系中,先描出点A(1,3),点B(4,1).并直接写出点A关于x轴的对称的A1的坐标A1 ( , ).
(2)在x轴上找一点C,使AC+BC的值最小; (保留作图痕迹).
(3)用尺规在x轴上找一点P,使PA=PB(保留作图痕迹).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=1,AD= ![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED,正确的个数是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED,正确的个数是( ) 
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山坡上有一颗树AB,树底部B点到山脚C点的距离BC为6 ![]() 米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将 ![]() ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将
ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将 ![]() CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).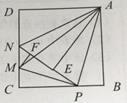
① ![]() CMP∽
CMP∽ ![]() BPA;
BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2 ![]() ;
;
⑤当 ![]() ABP≌
ABP≌ ![]() AND时,BP=4
AND时,BP=4 ![]() -4.
-4.
A.①②③
B.②③⑤
C.①④⑤
D.①②⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品每件成本10元,试销阶段每件产品的销售单价x(元/件)与日销售量y(件)之间的关系如下表.
x(元∕件) | 15 | 18 | 20 | 22 | … |
y(件) | 250 | 220 | 200 | 180 | … |
按照这样的规律可得,日销售利润w(元)与销售单价x(元/件)之间的函数关系式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,在Rt△ABC内部作正方形D1E1F1G1 , 其中点D1 , E1分别在AC,BC边上,边F1G1在BC上,它的面积记作S1;按同样的方法在△CD1E1内部作正方形D2E2F2G2 , 它的面积记作S2 , S2= , …,照此规律作下去,正方形DnEnFnGn的面积Sn= . 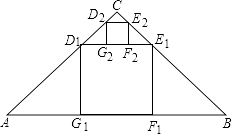
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com