
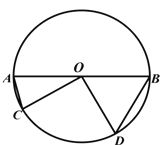
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() ,
,![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]()
![]() ,则
,则![]() 的半径为( )
的半径为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
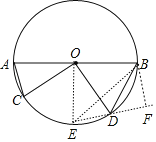
作半径OE⊥AB,连接DE,作BF⊥DE于F,如图,利用等角的余角相等得到∠DOE=∠AOC,则DE=AC=2,利用三角形内角和可计算出∠BDE=135°,所以∠BDF=45°,从而可计算出DF=BF=2,利用勾股定理计算出BE=2![]() ,然后根据△BOE为等腰直角三角形可得到OB的长.
,然后根据△BOE为等腰直角三角形可得到OB的长.
解:作半径OE⊥AB,连接DE,作BF⊥DE于F,如图,
∵∠DOC=90°,∠BOE=90°,
∴∠DOE=∠AOC,
∴DE=AC=2,
∵∠BDE=180°-![]() ×90°=135°,
×90°=135°,
∴∠BDF=45°,
∴DF=BF=![]()
在Rt△BEF,BE=![]() ,
,
∵△BOE为等腰直角三角形,
∴OB=![]()
.
故选:D.


科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
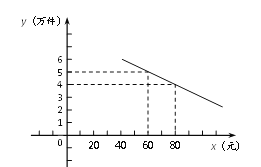
【题目】某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)为120万元,在销售过程中发现,年销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间存在着如图所示的一次函数关系.
(元)之间存在着如图所示的一次函数关系.
⑴ 直接写出![]() 关于
关于![]() 的函数关系式为 .
的函数关系式为 .
⑵ 市场管理部门规定,该产品销售单价不得超过100元,该公司销售该种产品当年获利55万元,求当年的销售单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
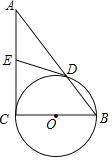
【题目】如图,在△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,⊙O的切线DE交AC于点E.
(1)求证:E是AC中点;
(2)若AB=10,BC=6,连接CD,OE,交点为F,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个袋中均有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标的数值分别为﹣7,﹣1,3,乙袋中的三张卡片上所标的数值分别为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用y表示取出的卡片上标的数值,把x、y分别作为点A的横坐标、纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况;
(2)求点A落在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,BC=2![]() .以BC的中点O为圆心的圆分别与AB,AC相切于D,E两点,则弧DE的长为( ).
.以BC的中点O为圆心的圆分别与AB,AC相切于D,E两点,则弧DE的长为( ).

A.![]() B.
B.![]() C.
C.![]() D.π
D.π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的直角顶点A在
的直角顶点A在![]() 轴上,OB=5,OA=4,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O运动,同时点N从点O出发,以每秒2个单位长度的速度,沿OB向终点B移动,当两个动点运动了
轴上,OB=5,OA=4,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O运动,同时点N从点O出发,以每秒2个单位长度的速度,沿OB向终点B移动,当两个动点运动了![]() 秒时,解答下列问题:
秒时,解答下列问题:
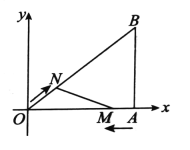
(1)若点B在反比例函数![]() 的图象上,求出该函数的解析式;
的图象上,求出该函数的解析式;
(2)在两个动点运动过程中,当![]() 为何值时,使得以O,M,N为顶点的三角形与
为何值时,使得以O,M,N为顶点的三角形与![]() 相似?
相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com