
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°∠ACB=60°.将Rt△ABC绕点C顺时针方向旋转后得到△DEC(△DEC≌△ABC),点E在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABF,连接AD.

(1)求证:四边形AFCD是菱形;
(2)连接BE并延长交AD于点G,连接CG.请问:四边形ABCG是什么特殊平行四边形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边AC,BC上,
分别在边AC,BC上,![]() ,连接BD,点F,P,G分别为AB,BD,DE的中点.
,连接BD,点F,P,G分别为AB,BD,DE的中点.
(1)如图1中,线段PF与PG的数量关系是 ,位置关系是 ;
(2)若把△ CDE绕点C逆时针方向旋转到图2的位置,连接AD,BE,GF,判断△ FGP的形状,并说明理由;
(3)若把△ CDE绕点C在平面内自由旋转,AC=8,CD=3,请求出△FGP面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
(1)画出将△ABC绕坐标原点O逆时针旋转90°图形.
(2)填空:以A、B、C为顶点的平行四边形的第四个顶点D的坐标为________.
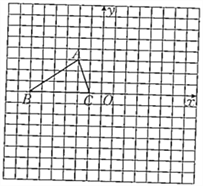
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)点P是x轴上的一动点,当PA+PB最小时,求点P的坐标;
(3)观察图象,直接写出不等式![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(选做题)包括两个小题,请选定其中一个小题用一元一次方程作答.
A.一根尼龙绳,小江第一次用去它的一半少![]() 米,第二次用去
米,第二次用去![]() 米,结果还剩下原来的
米,结果还剩下原来的![]() ,试问这根尼龙绳原来有多长?
,试问这根尼龙绳原来有多长?
B.小苏、小江家相距![]() 千米且附近均设有火车站,一列慢车从小江家附近的火车站驶往小苏家附近的火车站,速度为
千米且附近均设有火车站,一列慢车从小江家附近的火车站驶往小苏家附近的火车站,速度为![]()
![]() ,一列快车从小苏家附近的火车站驶往小江家附近的火车站,速度为
,一列快车从小苏家附近的火车站驶往小江家附近的火车站,速度为![]()
![]() ,若两车同时出发,多少时间后两车相距
,若两车同时出发,多少时间后两车相距![]()
![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() ,与y轴交于点B,抛物线
,与y轴交于点B,抛物线![]() 经过点
经过点![]() .
.
![]() 求k的值和抛物线的解析式;
求k的值和抛物线的解析式;
![]() 为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点
为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点![]() .
.
![]() 若以
若以![]() 为顶点的四边形OBNP是平行四边形时,求m的值.
为顶点的四边形OBNP是平行四边形时,求m的值.
![]() 连接BN,当
连接BN,当![]() 时,求m的值.
时,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com