
【题目】如图,分别以△ABC的边AB,AC向外作等边△ABD和等边△ACE,线段BE与CD相交于点O,连接OA.
(1)请你完成图形(尺规作图,不写作法,保留作图痕迹);

(2)求证:BE=DC;
(3)求证:OA平分∠DOE.
【答案】(1)图形见解析(2)证明见解析(3)证明见解析
【解析】试题分析:(1)先分别以点A、B为圆心,以AB为半径画弧,交于点D,连接AD、BC;再分别以点A、C为圆心,以AC为半径画弧,交于点E,连接AE、CE即可.
(2)根据等边三角形性质得出AB=AD,AE=AC,∠BAD=∠BDA=∠DBA=∠CAE=60°,求出∠BAE=∠DAC.根据SAS证△ABE≌△ADC即可.
(3)过点A分别作AM⊥BE,AN⊥DC,垂足为点M,N.根据三角形的面积公式求出AN=AM,根据角平分线性质求出即可.
试题解析:(1)完成图形,如图所示:
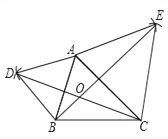
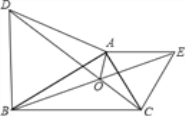
(2)证明:∵△ABD和△ACE都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠BDA=∠DBA=∠CAE=60°,
∴∠BAC+∠CAE=∠BAC+∠BAD,
即∠BAE=∠DAC,
在△ABE和△ADC中,
∵AB=AD,∠BAE=∠DAC,AE=AC,
∴△ABE≌△ADC(SAS),
∴BE=DC.
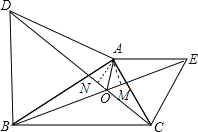
(3)证明:过点A分别作AM⊥BE,AN⊥DC,垂足为点M,N.
∵由(1)知:△ABE≌△ADC,
∴BE=DC,S△ABE=S△ADC,
∴![]() BEAM=
BEAM=![]() DCAN,
DCAN,
∴AM=AN,
∵AM⊥BE,AN⊥DC,
∴点A在∠DOE的平分线上,
即OA平分∠DOE.


科目:初中数学 来源: 题型:
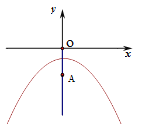
【题目】已知抛物线![]()
(1)填空:抛物线的顶点坐标是( , ),对称轴是 ;
(2)已知y轴上一点A(0,-2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点 N,使以点O、点A、点M、点N为顶点的四边形为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天小明和东东利用温差测量山峰的高度,东东在山脚下测得的温度是4℃,小明此时在山顶测得的温度是2℃,已知该地区高度每升高100米,气温下降0.8℃,这个山峰的高度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋中装有大小相同的2个红球和2个绿球.
(1)先从袋中摸出1个球后放回,混合均匀后再摸出1个球.求第一次摸到绿球,第二次摸到红球的概率;(用列表或数状图说明理由)
(2)先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据乘方运算,21=2,个位上的数字是2;22=4,个位上的数字是4;23=8,个位上的数字是8;24=16,个位上的数字是6;25=32,个位上的数字是2;……,按照此规律,22018的个位上的数字是( )
A. 2 B. 4 C. 8 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com