
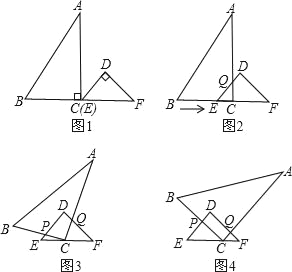
【题目】已知:RT△ABC与RT△DEF中,∠ACB=∠EDF=90°,∠DEF=45°,EF=8cm,AC=16cm,BC=12cm.现将RT△ABC和RT△DEF按图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,并按如下方式运动.
运动一:如图2,△ABC从图1的位置出发,以1cm/s的速度沿EF方向向右匀速运动,DE与AC相交于点Q,当点Q与点D重合时暂停运动;
运动二:在运动一的基础上,如图3,RT△ABC绕着点C顺时针旋转,CA与DF交于点Q,CB与DE交于点P,此时点Q在DF上匀速运动,速度为![]() cm/s,当QC⊥DF时暂停旋转;
cm/s,当QC⊥DF时暂停旋转;
运动三:在运动二的基础上,如图4,RT△ABC以1cm/s的速度沿EF向终点F匀速运动,直到点C与点F重合时为止.
设运动时间为t(s),中间的暂停不计时,
解答下列问题
(1)在RT△ABC从运动一到最后运动三结束时,整个过程共耗时 s;
(2)在整个运动过程中,设RT△ABC与RT△DEF的重叠部分的面积为S(cm2),求S与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)在整个运动过程中,是否存在某一时刻,点Q正好在线段AB的中垂线上,若存在,求出此时t的值;若不存在,请说明理由.
【答案】(1)10;(2)见解析;(3)存在,t=3.5或6﹣![]() 时,点Q正好在线段AB的中垂线上,理由见解析
时,点Q正好在线段AB的中垂线上,理由见解析
【解析】
(1)分段分别讨论分析;
(2) 动一,Rt△ABC与Rt△DEF的重叠部分为直角△QCE的面积,表示出即可;运动二,连接CD,可得∠E=∠CDQ,∠ECP=∠ECQ,EC=DC,所以△ECP≌△DCQ,RT△ABC与RT△DEF的重叠部分不变:y=8(4<t<6);运动三,四边形QDPC为矩形,CF=4-(t-6)=10-t,EC=8-CF=t-2,则可求得S矩形QDPC的值.
(3) Q在线段AB的中垂线上,连接BQ,可得AQ=QB,所以,AC-CQ=![]() ,又AC=16cm,BC=12cm,得,CQ=3.5cm,又由∠DEF=45°,所以,EC=3.5cm,解答出即可.
,又AC=16cm,BC=12cm,得,CQ=3.5cm,又由∠DEF=45°,所以,EC=3.5cm,解答出即可.
(1)根据题意得,
运动一:
∵△DEF是等腰三角形,∠ACB=90°,EF=8cm,
∴EC=4cm,
∴运动一所用时间为:4÷1=4(秒),
运动二:
∵当QC⊥DF时暂停旋转,
∵CD=CF,
∴DQ=QF=2![]() cm
cm
∴运动二所用时间为:2![]()
![]() =2(秒),
=2(秒),
运动三:
∵CF=4cm,
∴运动三所用的时间为:4÷1=4(秒),
∴整个过程共耗时4+2+4=10(秒);
故答案为:10;
(2)运动一:如图2,
设EC为tcm,则CQ为tcm,
∴S△ECQ=![]() ×t×t,
×t×t,
∴S与t之间的函数关系式为:y=![]() t2(0≤t≤4),
t2(0≤t≤4),
运动二:如图3,
连接CD,在△ECP和△DCQ中,
∵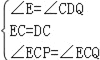
∴△ECP≌△DCQ(ASA),
∴S与t之间的函数关系式为:y=8(4<t<6),
运动三:如图4,
四边形QDPC为矩形,
∴CF=4﹣(t﹣6)=10﹣t,
EC=8﹣CF=t﹣2,
∴S矩形QDPC=![]() (t﹣2)×
(t﹣2)×![]() (10﹣t),
(10﹣t),
=![]() t2+6t﹣10;
t2+6t﹣10;
S与t之间的函数关系式为:y=![]() t2+6t﹣10(6≤t≤10);
t2+6t﹣10(6≤t≤10);
(3)存在点Q,理由如下:
如图5,运动一:
∵点Q在线段AB的中垂线上,连接BQ,
∴AQ=QB,
∴AC﹣CQ=![]() ,
,
又∵AC=16cm,BC=12cm,
解得,CQ=3.5cm,
∵∠DEF=45°,
∴EC=3.5cm,
此时,t为:3.5÷1=3.5秒.
如图6,运动二:
同理:CQ=3.5,
过点C作CM⊥DF交DF于点M,CM=2![]() ,
,
在Rt△QCM中,QM=![]() =
=![]() ,
,
∴DQ=2![]() ﹣
﹣![]() ,
,
∴t=(2![]() ﹣
﹣![]() )÷
)÷![]() +4=6﹣
+4=6﹣![]() ;
;
运动三时,CQ最大为2![]() <3.5,
<3.5,
所以无解.
综上,t=3.5或6﹣![]() 时,点Q正好在线段AB的中垂线上.
时,点Q正好在线段AB的中垂线上.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
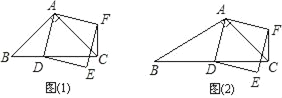
【题目】在△ABC中,∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC.如图①,且点D在线段BC上运动.试判断线段CF与BD之间的位置关系,并证明你的结论.
(2)如果AB≠AC,如图②,且点D在线段BC上运动.(1)中结论是否成立,为什么?
(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P,设AC=4![]() ,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图像如下图
所示:
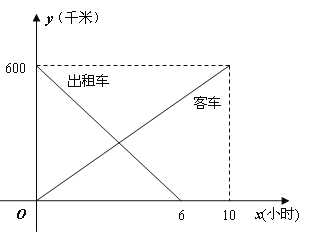
(1)根据图像,直接写出y1、y2关于x的函数关系式;
(2)若两车之间的距离为S千米,请写出S关于x的函数关系式;
(3)甲、乙两地间有A、B两个加油站,相距200千米,若客车进入A加油站时,出租车恰好进入B加油站,求A加油站离甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
(1)求证:![]() ;
;
(2)若AB⊥AC,AE:EC=1:2,F是BC中点,求证:四边形ABFD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论:
①只有一对相似三角形
②EF:ED=1:2
③S1:S2:S3:S4=1:2:4:5
其中正确的结论是( )
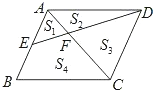
A.①③ B.③ C.① D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为( )
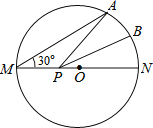
A. ![]() B. 1 C. 2 D.
B. 1 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,慢车的速度是快车速度的![]() ,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
根据图象解决以下问题:
(1)甲、乙两地之间的距离为 km;D点的坐标为 ;
(2)求线段BC的函数关系式,并写出自变量x的取值范围;
(3)若第二列快车从乙地出发驶往甲地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车追上慢车.求第二列快车比第一列快车晚出发多少小时?
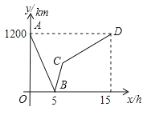
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com