
����Ŀ��һ���ͳ��Ӽؿ����ҵأ�һ��������ҵؿ����أ�����ͬʱ��������ͳ���صľ���Ϊy1ǧ�ף������صľ���Ϊy2ǧ�ף�������ʻ��ʱ��ΪxСʱ��y1��y2����x�ĺ���ͼ������ͼ
��ʾ��
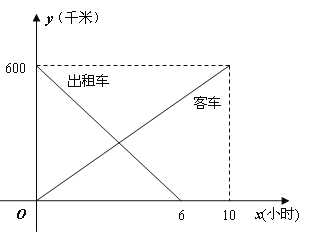
��1������ͼ��ֱ��д��y1��y2����x�ĺ�����ϵʽ��
��2��������֮��ľ���ΪSǧ�ף���д��S����x�ĺ�����ϵʽ��
��3���ס������ؼ���A��B��������վ�����200ǧ�ף����ͳ�����A����վʱ�����ǡ�ý���B����վ����A����վ��صľ���.
���𰸡���1��![]() ��0��x��10����
��0��x��10����![]() ��0��x��6����2��
��0��x��6����2��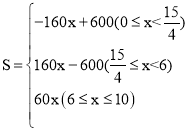 ��3��A����վ���ؾ���Ϊ150km��300km
��3��A����վ���ؾ���Ϊ150km��300km
��������
��1��ֱ�����ô���ϵ�����Ϳ������y1��y2����x�ĺ���ͼ��ϵʽ��
��2���ֱ���ݵ�0��x��![]() ʱ����
ʱ����![]() ��x��6ʱ����6��x��10ʱ��������ɣ�
��x��6ʱ����6��x��10ʱ��������ɣ�
��3����A����վ�ڼ���B����վ֮�䣬B����վ�ڼ���A����վ֮����������г�������⼴�ɣ�
��1����y1=k1x����ͼ��֪������ͼ���㣨10��600����
��10k1=600��
��ã�k1=60��
��y1=60x��0��x��10����
��y2=k2x+b����ͼ��֪������ͼ���㣨0��600������6��0������
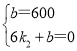 ��
��
��ã�![]()
��y2=-100x+600��0��x��6����
��2�������⣬��
60x=-100x+600
x=![]() ��
��
��0��x��![]() ʱ��S=y2-y1=-160x+600��
ʱ��S=y2-y1=-160x+600��
��![]() ��x��6ʱ��S=y1-y2=160x-600��
��x��6ʱ��S=y1-y2=160x-600��
��6��x��10ʱ��S=60x��
��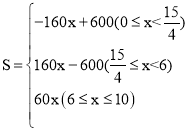 ��
��
��3�������⣬��
�ٵ�A����վ�ڼ���B����վ֮��ʱ����-100x+600��-60x=200��
���x=![]() ��
��
��ʱ��A����վ����أ�60��![]() =150km��
=150km��
�ڵ�B����վ�ڼ���A����վ֮��ʱ��60x-��-100x+600��=200��
���x=5����ʱ��A����վ����أ�60��5=300km��
����������A����վ���ؾ���Ϊ150km��300km��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
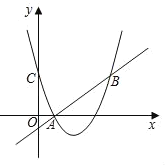
����Ŀ����ͼ�����κ���y����x��3��2+m��ͼ����y�ύ�ڵ�C����B�ǵ�C���ڸö��κ���ͼ��ĶԳ���ԳƵĵ㣬��֪һ�κ���y��kx+b��ͼ���ö��κ���ͼ���ϵĵ�A��1��0������B��
��1������κ�����һ�κ����Ľ���ʽ��
��2�����������Ƿ����һ��P��ʹS��ABP��S��ABC�������ڣ��������P�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
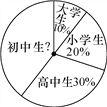
����Ŀ��ij��ѧ������Ӫ�����Сѧ�������������������ʹ�ѧ���μӣ���200�ˣ�����ѧ����������������ͳ��ͼ��
(1)�μ��������Ӫ��ij��������ж����ˣ�
(2)���֯�ߺ��ٲμ��������Ӫ�������ѧ��Ϊƶ��ѧ�������Сѧ��ÿ��
��� 5 Ԫ��������ÿ�˾�� 10 Ԫ��������ÿ�˾�� 15 Ԫ����ѧ��ÿ�˾�� 20 Ԫ����ƽ�� ÿ�˾���Ƕ���Ԫ��
(3)��(2)�������£���ÿ��ѧ���ľ������(��ԪΪ��λ)������¼�������������������У������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y��mx��3��ͼ����A(2��6)��B(n����3)����
(1)m��n��ֵ��
(2)��OAB�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ͼ�λͬѧ���ֵ�Ӱ����Ϸʱ�����ֶ���ͬһ���壬Ӱ�ӵĴ�С���Դ������ľ����й�.��ˣ�������Ϊ�����Խ��������Ӱ�ӳ��ȼ����Դ�������λ��.���ǣ������������³���.
��1����ͼ������ֱ�ڵ�����õ������ο��ABCD���߳�ABΪ30cm���������Ϸ���һ���ݣ��ڵ��ݵ������£������ο�ܵĺ���Ӱ��A��B��D��C�ij��Ⱥ�Ϊ6cm.��ô���������ĸ߶�Ϊ .
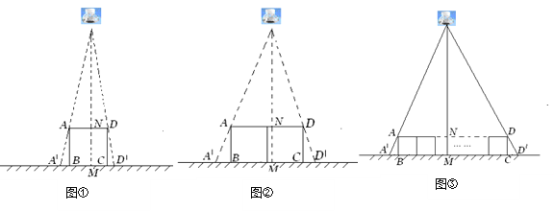 ��2�����ı����е��ݵĸ߶ȣ��������߳�Ϊ30cm�������ο�ܰ�ͼ���ڷţ�������ʱ����Ӱ��A��B��D��C�ij��Ⱥ�Ϊ���٣�
��2�����ı����е��ݵĸ߶ȣ��������߳�Ϊ30cm�������ο�ܰ�ͼ���ڷţ�������ʱ����Ӱ��A��B��D��C�ij��Ⱥ�Ϊ���٣�
��3����n���߳�Ϊa�������ΰ�ͼ���ڷţ���ú���Ӱ��A��B��D��C�ij��Ⱥ�Ϊb,����������ľ���.��д��������̣�����ú�a,b,n�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
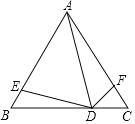
����Ŀ����ͼ��������ABC����D��E��F�ֱ���BC��AB��AC�ϣ��ҡ�BAC=��ADE=��ADF=60�㣮
��1����ͼ���ҳ����DAC��ȵĽǣ�������֤����
��2����AB=6��BE=m����AF���ú�m��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
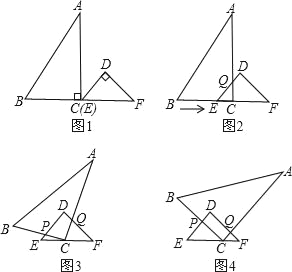
����Ŀ����֪��RT��ABC��RT��DEF�У���ACB����EDF��90������DEF��45����EF��8cm��AC��16cm��BC��12cm���ֽ�RT��ABC��RT��DEF��ͼ1�ķ�ʽ�ڷţ�ʹ��C���E�غϣ���B��C��E����F��ͬһ��ֱ���ϣ��������·�ʽ�˶���
�˶�һ����ͼ2����ABC��ͼ1��λ�ó�������1cm/s���ٶ���EF�������������˶���DE��AC�ཻ�ڵ�Q������Q���D�غ�ʱ��ͣ�˶���
�˶��������˶�һ�Ļ����ϣ���ͼ3��RT��ABC���ŵ�C˳ʱ����ת��CA��DF���ڵ�Q��CB��DE���ڵ�P����ʱ��Q��DF�������˶����ٶ�Ϊ![]() cm/s����QC��DFʱ��ͣ��ת��
cm/s����QC��DFʱ��ͣ��ת��
�˶��������˶����Ļ����ϣ���ͼ4��RT��ABC��1cm/s���ٶ���EF���յ�F�����˶���ֱ����C���F�غ�ʱΪֹ��
���˶�ʱ��Ϊt��s�����м����ͣ����ʱ��
�����������
��1����RT��ABC���˶�һ������˶�������ʱ���������̹���ʱ�� ��s��
��2���������˶������У���RT��ABC��RT��DEF���ص����ֵ����ΪS��cm2������S��t֮��ĺ�����ϵʽ����ֱ��д���Ա���t��ȡֵ��Χ��
��3���������˶������У��Ƿ����ijһʱ�̣���Q�������߶�AB���д����ϣ������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
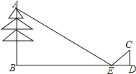
����Ŀ����ͼ��ʾ���ھ���![]() �ĵ�����ƽ��һ�澵��
�ĵ�����ƽ��һ�澵��![]() �����˺ྵ��
�����˺ྵ��![]() ��
��![]() �����ھ�����ǡ�ɿ���������������
�����ھ�����ǡ�ɿ���������������![]() �����
�����![]() �ף�
�ף�
![]() �����ߣ�
�����ߣ�
![]() ��
��![]() ��λ��ͼ�������ǣ���ָ��λ�����ģ������ǣ���˵�����ɣ�
��λ��ͼ�������ǣ���ָ��λ�����ģ������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BD��CE�ǡ�ABC�������ߣ�ֱ��BD��CE�ཻ�ڵ�H.

(1)����BAC��100�㣬���DHE�Ķ�����
(2)����ABC�С�BAC��50�㣬ֱ��д����DHE�Ķ�����____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com