
【题目】如图,等腰△ABC,点D、E、F分别在BC、AB、AC上,且∠BAC=∠ADE=∠ADF=60°.
(1)在图中找出与∠DAC相等的角,并加以证明;
(2)若AB=6,BE=m,求:AF(用含m的式子表示).
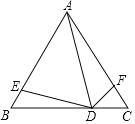
【答案】(1)∠BDE=∠DAC,证明见解析;(2)AF=6﹣m.
【解析】
(1)首先证明△ABC是等边三角形,再利用三角形的外角的性质解决问题即可.
(2)在DE上截取DG=DF,连接AG,先判定△ADG≌△ADF,得到AG=AF,再根据∠AEG=∠AGE,得出AE=AG,进而得到AE=AF即可解决问题.
解:(1)结论:∠BDE=∠DAC.
理由:∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴∠C=60°.
∵∠ADB=∠3+∠ADE=∠1+∠C,∠ADE=∠C=60°,
∴∠3=∠1.
(2)如图,在DE上截取DG=DF,连接AG.

∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵∠ADE=∠ADF=60°,AD=AD,
∴△ADG≌△ADF(SAS),
∴AG=AF,∠1=∠2.
∵∠3=∠1,
∴∠3=∠2
∵∠AEG=60°+∠3,∠AGE=60°+∠2,
∴∠AEG=∠AGE,
∴AE=AG,
∴AE=AF=6﹣m.


科目:初中数学 来源: 题型:
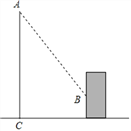
【题目】小左同学想利用影长测量学校旗杆的高度,如图,她在某一时刻立一长度为1米的标杆,测得其影长为![]() 米,同时旗杆投影的一部分在地上,另一部分在某一建筑物的墙上,测得旗杆与建筑物的距离为10米,旗杆在墙上的影高为2米,请帮小左同学算出学校旗杆的高度.
米,同时旗杆投影的一部分在地上,另一部分在某一建筑物的墙上,测得旗杆与建筑物的距离为10米,旗杆在墙上的影高为2米,请帮小左同学算出学校旗杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
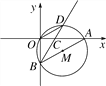
【题目】如图,在直角坐标系中,⊙M经过原点O(0,0),点A(![]() ,0)与点B(0,-
,0)与点B(0,-![]() ),点D在劣弧
),点D在劣弧![]() 上,连结BD交x轴于点C,且∠COD=∠CBO.
上,连结BD交x轴于点C,且∠COD=∠CBO.
(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰为⊙M的切线,求此时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的圆形纸片进行如下设计:
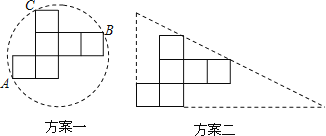
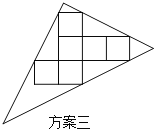
说明:方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点.
纸片利用率=![]() ×100%
×100%
发现:(1)方案一中的点A、B恰好为该圆一直径的两个端点.
你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.
请帮忙计算方案二的利用率,并写出求解过程.
探究:
(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图像如下图
所示:
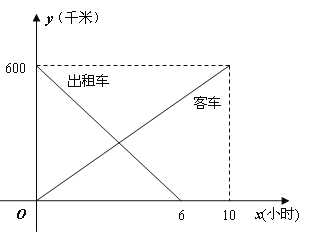
(1)根据图像,直接写出y1、y2关于x的函数关系式;
(2)若两车之间的距离为S千米,请写出S关于x的函数关系式;
(3)甲、乙两地间有A、B两个加油站,相距200千米,若客车进入A加油站时,出租车恰好进入B加油站,求A加油站离甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结论:直角三角形中,![]() 的锐角所对的直角边等于斜边的一半.
的锐角所对的直角边等于斜边的一半.
如图①,我们用几何语言表示如下:
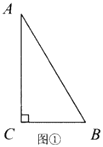
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
你可以利用以上这一结论解决以下问题:
如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
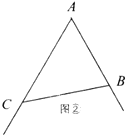
(1)求![]() 的面积;
的面积;
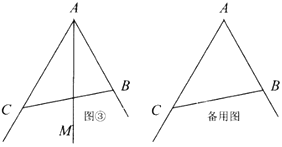
(2)如图③,射线![]() 平分
平分![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着射线
出发,以每秒1个单位的速度沿着射线![]() 的方向运动,过点
的方向运动,过点![]() 分别作
分别作![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒,当
秒,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.
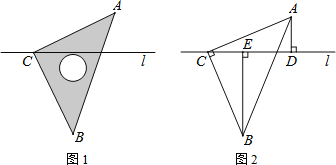
(1)△ACD与△CBE全等吗?说明你的理由.
(2)猜想线段AD、BE、DE之间的关系.(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com