
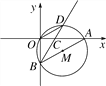
【题目】如图,在直角坐标系中,⊙M经过原点O(0,0),点A(![]() ,0)与点B(0,-
,0)与点B(0,-![]() ),点D在劣弧
),点D在劣弧![]() 上,连结BD交x轴于点C,且∠COD=∠CBO.
上,连结BD交x轴于点C,且∠COD=∠CBO.
(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰为⊙M的切线,求此时点E的坐标.
【答案】(1)M的半径r=![]() ;(2)证明见解析;(3)点E的坐标为(
;(2)证明见解析;(3)点E的坐标为(![]() ,
,![]() ).
).
【解析】试题分析:根据点A和点B的坐标得出OA和OB的长度,根据Rt△AOB的勾股定理得出AB的长度,然后得出半径;根据同弧所对的圆周角得出∠ABD=∠COD,然后结合已知条件得出角平分线;根据角平分线得出△ABE≌△HBE,从而得出BH=BA=2![]() ,从而求出OH的长度,即点E的纵坐标,根据Rt△AOB的三角函数得出∠ABO的度数,从而得出∠CBO的度数,然后根据Rt△HBE得出HE的长度,即点E的横坐标.
,从而求出OH的长度,即点E的纵坐标,根据Rt△AOB的三角函数得出∠ABO的度数,从而得出∠CBO的度数,然后根据Rt△HBE得出HE的长度,即点E的横坐标.
试题解析:(1)∵点A为(![]() ,0),点B为(0,-
,0),点B为(0,-![]() ) ∴OA=
) ∴OA=![]() OB=
OB=![]()
∴根据Rt△AOB的勾股定理可得:AB=2![]() ∴
∴![]() M的半径r=
M的半径r=![]() AB=
AB=![]() .
.
(2)根据同弧所对的圆周角相等可得:∠ABD=∠COD ∵∠COD=∠CBO ∴∠ABD=∠CBO
∴BD平分∠ABO
(3)如图,由(2)中的角平分线可得△ABE≌△HBE ∴BH=BA=2![]() ∴OH=2
∴OH=2![]() -
-![]() =
=![]()
在Rt△AOB中,![]() ∴∠ABO=60° ∴∠CBO=30°
∴∠ABO=60° ∴∠CBO=30°
在Rt△HBE中,HE=![]() ∴点E的坐标为(
∴点E的坐标为(![]() ,
,![]() )
)



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( ) 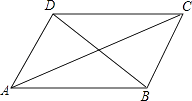
A.①②
B.②③
C.①③
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() .
.
(1)若该反比例函数的图象与直线![]() (
(![]() ≠0)只有一个公共点,求
≠0)只有一个公共点,求![]() 的值;
的值;
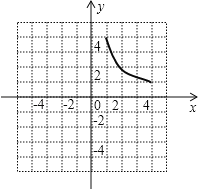
(2)如图,反比例函数![]() 的图象记为曲线
的图象记为曲线![]() ,将
,将![]() 向左平移2个单位长度,得曲线
向左平移2个单位长度,得曲线![]() ,请在图中画出
,请在图中画出![]() ,并直接写出
,并直接写出![]() 平移至
平移至![]() 处 所扫过的面积.
处 所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,能够进入人体的肺部危害身体健康.检测PM2.5指数在一年中最可靠的一种观测方法是( )
A. 随机选择5天进行观测
B. 选择某个月进行连续观测
C. 选择在春节7天期间连续观测
D. 每个月都随机选中5天进行观测
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE. 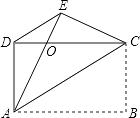
(1)求证:△ADE≌△CED;
(2)求证:DE∥AC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com