
【题目】如图,已知BD,CE是△ABC的两条高,直线BD,CE相交于点H.

(1)若∠BAC=100°,求∠DHE的度数;
(2)若△ABC中∠BAC=50°,直接写出∠DHE的度数是____.
【答案】(1)∠DHE=80°(2)50°或130°
【解析】
(1)根据已知条件可得∠HDA=∠AEH=90°,根据对顶角相等可得∠DAE的度数;
再根据四边形的内角和是360°便求出∠DHE的度数;
(2)需分两种情况讨论:当△ABC为锐角三角形时和当△ABC为钝角三角形时,分别求出∠DHE的度数即可.
(1)∵BD、CE是△ABC的两条高,
∴∠HDA=∠AEH=90°,
∵∠BAC=100°,
∴∠DAE=∠BAC=100°,
∴在四边形AEHD中,∠DHE=360°-∠HDA-∠DAE-∠AEH=80°,
(2)①当△ABC为锐角三角形时,∠DHE=180°-50°=130°,
②当△ABC为钝角三角形时,∠DHE=∠BAC=50°,
∴∠DHE的度数为130°或50°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图像如下图
所示:
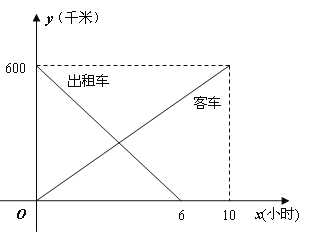
(1)根据图像,直接写出y1、y2关于x的函数关系式;
(2)若两车之间的距离为S千米,请写出S关于x的函数关系式;
(3)甲、乙两地间有A、B两个加油站,相距200千米,若客车进入A加油站时,出租车恰好进入B加油站,求A加油站离甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为( )
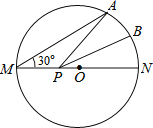
A. ![]() B. 1 C. 2 D.
B. 1 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,![]() ,
,![]() ,
,![]() ,对角线BD平分
,对角线BD平分![]() 交AC于点P.CE是
交AC于点P.CE是![]() 的角平分线,交BD于点O.
的角平分线,交BD于点O.
(1)请求出![]() 的度数;
的度数;
(2)试用等式表示线段BE、BC、CP之间的数量关系,并说明理由;
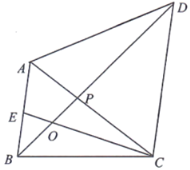
查看答案和解析>>
科目:初中数学 来源: 题型:
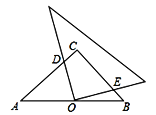
【题目】如图,在等腰直角![]() 中,
中, ![]() ,点
,点![]() 是
是![]() 的中点,且AC=3,将一块直角三角板的直角顶点放在点
的中点,且AC=3,将一块直角三角板的直角顶点放在点![]() 处,始终保持该直角三角板的两直角边分别与
处,始终保持该直角三角板的两直角边分别与![]() 、
、![]() 相交,交点分别为
相交,交点分别为![]() 、
、![]() ,则
,则![]() ___________.
___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.
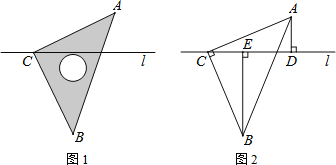
(1)△ACD与△CBE全等吗?说明你的理由.
(2)猜想线段AD、BE、DE之间的关系.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
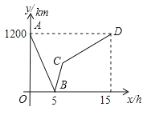
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,慢车的速度是快车速度的![]() ,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
根据图象解决以下问题:
(1)甲、乙两地之间的距离为 km;D点的坐标为 ;
(2)求线段BC的函数关系式,并写出自变量x的取值范围;
(3)若第二列快车从乙地出发驶往甲地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车追上慢车.求第二列快车比第一列快车晚出发多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣1 | ﹣ | ﹣2 | ﹣ | … |
根据表格中的信息,完成下列各题:
(1)当x=3时,y=________;
(2)当x=_____时,y有最________值为________;
(3)若点A(x1,y1)、B(x2,y2)是该二次函数图象上的两点,且﹣1<x1<0,1<x2<2,试比较两函数值的大小:y1________y2 ;
(4)若自变量x的取值范围是0≤x≤5,则函数值y的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com