练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

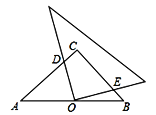
    【题目】如图，在等腰直角中， ，点是的中点，且AC=3，将一块直角三角板的直角顶点放在点处，始终保持该直角三角板的两直角边分别与、相交，交点分别为、，则___________．

    【答案】3

    【解析】

    连接CO，结合等腰直角三角形的性质可证明△ADO≌△COE，可证得AD=CE，则可求得CD+CE=AC=3．

    如图，连接CO，

    ∵在等腰直角△ABC中，∠C=90°，点O是AB的中点，

    ∴CO=AO，∠A=∠OCB=45°，且∠AOC=90°，

    ∵∠DOE=90°，

    ∴∠AOD+∠DOC=∠DOC+∠COE=90°，

    ∴∠AOD=∠COE，

    在△ADO和△COE中

    ∵∠A=∠OCE，AO=CO，∠AOD=∠COE

    ∴△ADO≌△COE(ASA)，

    ∴AD=CE，

    ∴CD+CE=CD+AD=AC=3，

    故答案为：3.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关.因此，他们认为：可以借助物体的影子长度计算光源到物体的位置.于是，他们做了以下尝试.

    （1）如图①，垂直于地面放置的正方形框架ABCD，边长AB为30cm，在其正上方有一灯泡，在灯泡的照射下，正方形框架的横向影子A′B，D′C的长度和为6cm.那么灯泡离地面的高度为 .

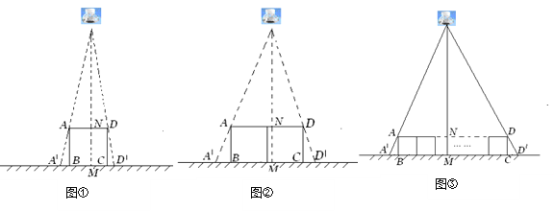    （2）不改变①中灯泡的高度，将两个边长为30cm的正方形框架按图②摆放，请计算此时横向影子A′B，D′C的长度和为多少？

    （3）有n个边长为a的正方形按图③摆放，测得横向影子A′B，D′C的长度和为b,求灯泡离地面的距离.（写出解题过程，结果用含a,b,n的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在某隧道建设工程中，需沿方向开山修路，为了加快施工进度，要在小山的另一边同时施工．为了使开挖点在直线上，现在上取一点，外取一点，测得，，．求开挖点到点的距离．

    （精确到米）参考数据：，，．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1是一辆吊车的实物图，图2是其工作示意图，AC是可以伸缩的起重臂，其转动点A离地面BD的高度AH为3.4m．当起重臂AC长度为9m，张角∠HAC为118°时，求操作平台C离地面的高度（结果保留小数点后一位：参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解某区八年级学生的睡眠情况，随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人，利用抽样所得的数据绘制所示的统计图表.

    一、学生睡眠情况分组表（单位：小时）

    组别

    睡眠时间

    二、学生睡眠情况统计图

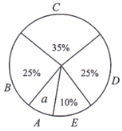
    根据图表提供的信息，回答下列问题：

    （1）试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数；

    （2）如果睡眠时间x（时）满足：，称睡眠时间合格.已知该区八年级学生有3250人，试估计该区八年级学生睡眠时间合格的共有多少人？

    （3）如果将各组别学生睡眠情况分组的最小值（如C组别中，取），B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知BD，CE是△ABC的两条高，直线BD，CE相交于点H.

    (1)若∠BAC＝100°，求∠DHE的度数；

    (2)若△ABC中∠BAC＝50°，直接写出∠DHE的度数是____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，G是边长为4的正方形ABCD的边BC上的一点，矩形DEFG的边EF过A，GD=5．

    （1）指出图中所有的相似三角形；

    （2）求FG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

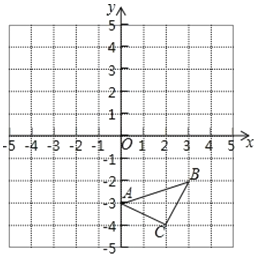
    【题目】如图，在平面直角坐标系中，△ABC 的顶点坐标分别为A（0，-3），B（3，-2），C（2，-4）．

    （1）在图中作出△ABC关于x轴对称的△A1B1C1．

    （2）点C1的坐标为：　　　　 ．

    （3）△ABC的周长为　　　　 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

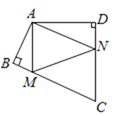
    【题目】如图，在四边形ABCD中，∠BAD=130°，∠B=∠D=90°，在BC，CD上分别找一点M，N，使三角形AMN周长最小时，则∠MAN的度数为_________.

    查看答案和解析>>

    同步练习册答案